江苏省无锡新吴区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 下列图形中,哪一个是圆锥的侧面展开图?( )A、
 B、
B、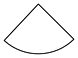 C、
C、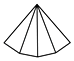 D、
D、 2. 下列运算正确的是A、 B、 C、 D、3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000人,这个数用科学记数法表示为( )A、44×108 B、4.4×108 C、4.4×109 D、4.4×10104. 一元一次方程3x+6=2x﹣8移项后正确的是( )A、3x﹣2x=6﹣8 B、3x﹣2x=﹣8+6 C、3x﹣2x=8﹣6 D、3x﹣2x=﹣6﹣85. 在-(-8),(-1)2007 , -32 , -|-1|,-|0|,- , 中,负有理数共有( )A、4个 B、3个 C、2个 D、1个6. 下列说法中正确的是A、过一点有且仅有一条直线与已知直线平行 B、若 ,则点C是线段AB的中点 C、两点之间的所有连线中,线段最短 D、相等的角是对顶角7. 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图①变到图②,不改变的是( )
2. 下列运算正确的是A、 B、 C、 D、3. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000人,这个数用科学记数法表示为( )A、44×108 B、4.4×108 C、4.4×109 D、4.4×10104. 一元一次方程3x+6=2x﹣8移项后正确的是( )A、3x﹣2x=6﹣8 B、3x﹣2x=﹣8+6 C、3x﹣2x=8﹣6 D、3x﹣2x=﹣6﹣85. 在-(-8),(-1)2007 , -32 , -|-1|,-|0|,- , 中,负有理数共有( )A、4个 B、3个 C、2个 D、1个6. 下列说法中正确的是A、过一点有且仅有一条直线与已知直线平行 B、若 ,则点C是线段AB的中点 C、两点之间的所有连线中,线段最短 D、相等的角是对顶角7. 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图①变到图②,不改变的是( ) A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图8. 如图,某商品实施促销“第二件半价”,若购买2件该商品,则相当于这2件商品共打了( )
A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图8. 如图,某商品实施促销“第二件半价”,若购买2件该商品,则相当于这2件商品共打了( ) A、5折 B、5.5折 C、7折 D、7.5折9. 已知线段 ,在直线AB上取一点P,恰好使 ,点Q为PB的中点,则线段AQ的长是A、5cm B、9cm C、5cm或9cm D、3cm或5cm10. 如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.
A、5折 B、5.5折 C、7折 D、7.5折9. 已知线段 ,在直线AB上取一点P,恰好使 ,点Q为PB的中点,则线段AQ的长是A、5cm B、9cm C、5cm或9cm D、3cm或5cm10. 如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.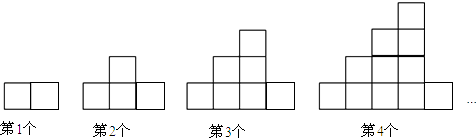 A、156 B、157 C、158 D、159
A、156 B、157 C、158 D、159二、填空题
-
11. 代数式 与 的和是一个单项式,则 .12. 已知 ,则 的补角为.13. 若a2﹣3b=4,则3b﹣a2+2018=.14. 已知关于x的方程(k﹣1)x|k|﹣1=0是一元一次方程,则k的值为 .15.
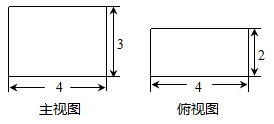
长方体的主视图与俯视图如图所示,则这个长方体的体积是.
 16. 已知 ,自 的顶点O引射线OC,若 : :5,则 的度数是.17. 任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数0. 为例进行说明:设0. =x,由0. =0.7777…可知,10x=7.7777…,所以10x﹣x=7,解方程,得x= ,于是.得0. = .将0. 写成分数的形式是.18. 下面是一种利用图形计算正整数乘法的方法,请根据图1﹣图4四个算图所示的规律,可知图5所表示的等式为。
16. 已知 ,自 的顶点O引射线OC,若 : :5,则 的度数是.17. 任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数0. 为例进行说明:设0. =x,由0. =0.7777…可知,10x=7.7777…,所以10x﹣x=7,解方程,得x= ,于是.得0. = .将0. 写成分数的形式是.18. 下面是一种利用图形计算正整数乘法的方法,请根据图1﹣图4四个算图所示的规律,可知图5所表示的等式为。
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 先化简,后求值:(3a2﹣4ab)﹣2(a2+2ab),其中a,b满足|a+1|+(2﹣b)2=0.22. 利用网格画图:
 (1)、①过点C画AB的平行线;
(1)、①过点C画AB的平行线;②过点C画AB的垂线,垂足为E;
(2)、连接CA、CB,在线段CA、CB、CE中,线段最短,理由:;(3)、点C到直线AB的距离线段CE的长度.
23. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件.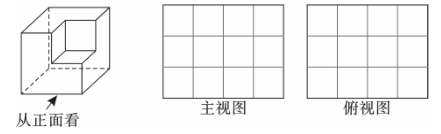 (1)、这个零件的表面积是;(2)、请在边长为1的网格图里画出这个零件的主视图和俯视图.24.
(1)、这个零件的表面积是;(2)、请在边长为1的网格图里画出这个零件的主视图和俯视图.24.如图,线段 AB 的中点为 M,C 点将线段 MB 分成 MC:CB=1:3 的两段,若 AC=10,求AB 的长.
 25. 如图,直线AB,CD相交于点O,OE平分 , ,
25. 如图,直线AB,CD相交于点O,OE平分 , , (1)、图中 的余角是 把符合条件的角都填出来 ;(2)、如果 ,那么根据可得 度;(3)、如果 ,求 和 的度数.26. 图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示);使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50 cm,第2节套管长46 cm,以此类推,每一节套管均比前一节套管少4 cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为x cm.
(1)、图中 的余角是 把符合条件的角都填出来 ;(2)、如果 ,那么根据可得 度;(3)、如果 ,求 和 的度数.26. 图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示);使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50 cm,第2节套管长46 cm,以此类推,每一节套管均比前一节套管少4 cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为x cm. (1)、请直接写出第5节套管的长度;(2)、当这根鱼竿完全拉伸时,其长度为311 cm,求x的值.27. 如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)、请直接写出第5节套管的长度;(2)、当这根鱼竿完全拉伸时,其长度为311 cm,求x的值.27. 如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问: (1)、用含t的代数式表示动点P在运动过程中距O点的距离;(2)、P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?(3)、是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.
(1)、用含t的代数式表示动点P在运动过程中距O点的距离;(2)、P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?(3)、是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.