江苏省南通市通州区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. $- 3$ 的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 港珠澳大桥是连接香港、珠海、澳门的超大型跨海通道，全长约55000米，把55000用科学记数法表示为（）

A、55×10³ B、5.5×10⁴ C、5.5×10⁵ D、0.55×10⁵

查看试题解析
3. 化简下列式子结果为负数的是 $($ $)$

A、 $| - 2 |$ B、 $- (- 2)$ C、 $2^{- 1}$ D、 $- 2^{2}$

查看试题解析
4. 下列计算正确的是（）

A、3xy﹣2yx=xy B、5y﹣3y=2 C、7a+a=7a² D、3a+2b=5ab

查看试题解析
5. 下图中的图形绕虚线旋转一周，可得到的几何体是（）

A、 B、 C、 D、

查看试题解析
6. 已知有理数m、n在数轴上的对应点的位置如图所示，则下列判断正确的是（）。

A、 $| m |$ <1 B、n>1 C、mn<0 D、m-n>0

查看试题解析
7. 如图所示，点E在AB的延长线上，下列条件中不能判断AB//CD的是（）

A、∠1＝∠2 B、∠3＝∠4 C、∠C＝∠CBE D、∠C+∠ABC＝180°

查看试题解析
8. 下列说法正确的是（）

A、有公共顶点且相等的两个角是对顶角 B、已知线段AB＝BC，则点B是线段AC的中点 C、经过一点有且只有一条直线与已知直线平行 D、在同一平面内，经过一点有且只有一条直线与已知直线垂直

查看试题解析
9. 在古代生活中，有很多时候也要用到不少的数学知识，比如有这样一道题：隔墙听得客分银，不知人数不知银 $.$ 七两分之多四两，九两分之少半斤 $. ($ 注：古秤十六两为一斤 $)$ 请同学们想想有几人，几两银？ $($ ）

A、六人，四十四两银 B、五人，三十九两银 C、六人，四十六两银 D、五人，三十七两银

查看试题解析
10. 找出以如图形变化的规律，则第2019个图形中黑色正方形的数量是 $($ $)$

A、2019 B、3027 C、3028 D、3029

查看试题解析

二、填空题

11. 用“＞”或“＜”填空：比较大小：－ $\frac{1}{2}$ － $\frac{2}{3}$ .

查看试题解析
12. 若 $2 x - 3 y + 3 = 0$ ，则 $5 - 4 x + 6 y =$ .

查看试题解析
13. 若 $∠ a = 70^{\circ} 42'$ ，则 $∠ a$ 的余角等于.

查看试题解析
14. 若 ${(x + 2)}^{2} + | y + 3 | = 0$ ，则 $y^{x}$ 的值是.

查看试题解析
15. 如图，在长方形ABCD中，AB=10cm，BC=6cm，若此长方形以2cm/s的速度沿着A→B方向移动，经过秒平移后的长方形与原来长方形重叠部分的面积为24cm².

查看试题解析
16. 如图，线段 $AB = 12 cm$ ，C是线段AB上任意一点，M，N分别是AC，BC的中点，MN的长为cm.

查看试题解析
17. 如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD＝95°，∠CDE＝25°，则∠DEF=度.

查看试题解析
18. 若关于x的一元一次方程 $\frac{1}{2018}$ x-2=3x+k的解为x=-5，则关于y的一元一次方程 $\frac{1}{2018}$ （2y+1）-5=6y+k的解y=.

查看试题解析

三、解答题

19. 计算

(1)、 $- \frac{3}{2} \times (- \frac{1}{2} + \frac{5}{6} - 4)$ ；

(2)、 $- 1^{4} - (1 - 0.5) \times \frac{1}{3} \times [2 - (- 3)^{2}] .$

查看试题解析
20. 先化简，再求值： $x + 2 (3 y^{2} - 2 x) - 4 (2 x - y^{2})$ ，其中 $x = 2$ ， $y = - 1$ .

查看试题解析
21. 一商店在某一时间以每件a元（a＞0）的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%.

(1)、当a=60时，分析卖出这两件衣服总的是盈利还是亏损，或是不盈不亏？

(2)、小安发现：不论a为何值，这样卖两件衣服总的都是亏损.请判断“小安发现”是否正确？

查看试题解析
22.

(1)、 $4 - 4 (x - 3) = 2 (9 - x)$ ；

(2)、 $\frac{2 - x}{2} - \frac{x - 1}{3} = 1$ .

查看试题解析
23. 如图，点C在线段AB上，AC= $\frac{1}{2}$ BC，点D是线段AB的中点，若AD=3，求线段CD的长.

查看试题解析
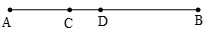24. 如图，点A，O，B在同一直线上，射线OD和射线OE分别平分∠AOC和∠BOC.

(1)、当∠BOE=25°时，求∠AOD的度数

(2)、在图中找出∠COD的补角，并说明理由.

查看试题解析
25. 如图，所有小正方形的边长都为1，A、B、C都在格点上.

(1)、①过点C画直线AB的平行线（不写画法，下同）；
②过点A画直线BC的垂线，并注明垂足为G；过点A画直线AB的垂线，交BC于点H.

(2)、线段的长度是点A到直线BC的距离；

(3)、线段AG、AH的大小关系为AGAH.（填“＞”或“＜”或“＝”），理由.

查看试题解析
26. 如图，D，E分别是三角形ABC的边AB，BC上的点，DE∥AC，点F在DE的延长线上，且∠DFC＝∠A.

(1)、求证：AB∥CF；

(2)、若∠ACF比∠BDE大40°，求∠BDE的度数.

查看试题解析
27. 如图1，射线OC在 $∠ AOB$ 的内部，图中共有3个角： $∠ AOB$ 、 $∠ AOC$ 和 $∠ BOC$ ，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是 $∠ AOB$ 的“定分线”

(1)、一个角的平分线这个角的“定分线”； $($ 填“是”或“不是” $)$

(2)、如图2，若 $∠ MPN = a$ ，且射线PQ是 $∠ MPN$ 的“定分线”，则 $∠ MPQ =$ $($ 用含a的代数式表示出所有可能的结果 $)$

(3)、如图2，若 $∠ MPN = 45^{\circ}$ ，且射线PQ绕点P从PN位置开始，以每秒 $10^{\circ}$ 的速度逆时针旋转，当PQ与PN成 $90^{\circ}$ 时停止旋转，旋转的时间为t秒 $.$ 同时射线PM绕点P以每秒 $5^{\circ}$ 的速度逆时针旋转，并与PQ同时停止 $.$ 当PQ是 $∠ MPN$ 的“定分线”时，求t的值.

查看试题解析