江苏省南京市江宁区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 如图是我市十二月份某一天的天气预报,该天的温差是
 A、 B、 C、 D、2. 若足球质量与标准质量相比,超出部分记作正数,不足部分记作负数,则在下面4个足球中,质量最接近标准的是A、
A、 B、 C、 D、2. 若足球质量与标准质量相比,超出部分记作正数,不足部分记作负数,则在下面4个足球中,质量最接近标准的是A、 B、
B、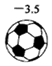 C、
C、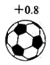 D、
D、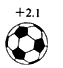 3. 下列运算正确的是A、 B、 C、 D、4. 如图,用剪刀沿直线将一片平整的长方形纸片剪掉一部分,发现剩下纸片的周长比原纸片的周长要小,能正确解释这一现象的数学知识是
3. 下列运算正确的是A、 B、 C、 D、4. 如图,用剪刀沿直线将一片平整的长方形纸片剪掉一部分,发现剩下纸片的周长比原纸片的周长要小,能正确解释这一现象的数学知识是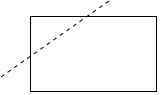 A、经过两点,有且仅有一条直线 B、经过一点有无数条直线 C、两点之间,线段最短 D、垂线段最短5. 如图是一个正方体的展开图,折好以后与“学”相对面上的字是( )
A、经过两点,有且仅有一条直线 B、经过一点有无数条直线 C、两点之间,线段最短 D、垂线段最短5. 如图是一个正方体的展开图,折好以后与“学”相对面上的字是( )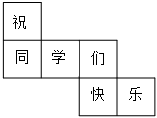 A、祝 B、同 C、快 D、乐6. 射线OC在∠AOB的内部,下列给出的条件中不能得出OC是∠AOB的平分线的是( )A、∠AOC=∠BOC B、∠AOC+∠BOC=∠AOB C、∠AOB=2∠AOC D、∠BOC= ∠AOB7. 如图,点C是射线OA上一点,过C作CD⊥OB,垂足为D,作CE⊥OA,垂足为C,交OB于点E.给出下列结论:①∠1是∠DCE的余角;②∠AOB=∠DCE;③图中互余的角共有3对;④∠ACD=∠BEC.其中正确结论有( )
A、祝 B、同 C、快 D、乐6. 射线OC在∠AOB的内部,下列给出的条件中不能得出OC是∠AOB的平分线的是( )A、∠AOC=∠BOC B、∠AOC+∠BOC=∠AOB C、∠AOB=2∠AOC D、∠BOC= ∠AOB7. 如图,点C是射线OA上一点,过C作CD⊥OB,垂足为D,作CE⊥OA,垂足为C,交OB于点E.给出下列结论:①∠1是∠DCE的余角;②∠AOB=∠DCE;③图中互余的角共有3对;④∠ACD=∠BEC.其中正确结论有( )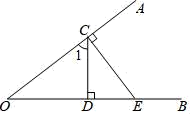 A、①②③ B、①②④ C、①③④ D、②③④8. 如图,“ 、 、 ”分别表示三种不同的物体 已知前两架天平保持平衡,要使第三架也保持平衡 如果在“?”处只放“ ”,那么应放“ ”
A、①②③ B、①②④ C、①③④ D、②③④8. 如图,“ 、 、 ”分别表示三种不同的物体 已知前两架天平保持平衡,要使第三架也保持平衡 如果在“?”处只放“ ”,那么应放“ ” A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
9. 的相反数是 , 的倒数是.10. 十一黄金周,南京市七大旅游景区共接待国内外游客约4 490 000人次,将4 490 000用科学记数法可以表示为.11. 已知方程2x+y=3,用含x的代数式表示y,则y=.12. 若 ,则 的余角为13. 已知 是关于x的方程 的根,则a的值是.14. 若x,y满足方程组 ,则 .15. 如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=.
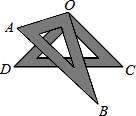 16. 已知 ,自 的顶点O引射线OC,若 : :3,那么 的度数是.17. 如图,如果圆环外圆的周长比内圆的周长长2m,那么外圆的半径比内圆的半径大 结果保留
16. 已知 ,自 的顶点O引射线OC,若 : :3,那么 的度数是.17. 如图,如果圆环外圆的周长比内圆的周长长2m,那么外圆的半径比内圆的半径大 结果保留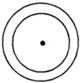 18. 如图,将一张长为17,宽为11的长方形纸片,去掉阴影部分,恰可以围成一个宽是高2倍的长方体纸盒,这个长方体纸盒的容积是.
18. 如图,将一张长为17,宽为11的长方形纸片,去掉阴影部分,恰可以围成一个宽是高2倍的长方体纸盒,这个长方体纸盒的容积是.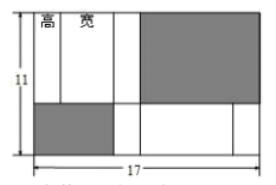
三、解答题
-
19. 计算(1)、 ;(2)、 .20. 解方程 组(1)、 ;(2)、21. 先化简,再求值: ,其中 , .22. 对于三个数a,b,c,用 b, 表示a,b,c这三个数的平均数,用 b, 表示a,b,c这三个数中最小的数,如: 2, , 2, .(1)、若 ,求x的值;(2)、已知 , 0, ,是否存在一个x值,使得 0, 若存在,请求出x的值;若不存在,请说明理由.23. 将一副三角板如图1摆放在直线MN上,在三角板OAB和三角板OCD中, , , .
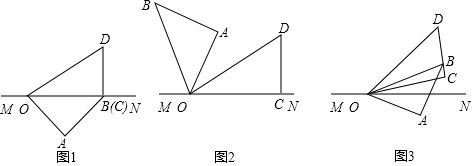 (1)、保持三角板OCD不动,将三角板OAB绕点O以每秒 的速度逆时针旋转,旋转时间为t秒.
(1)、保持三角板OCD不动,将三角板OAB绕点O以每秒 的速度逆时针旋转,旋转时间为t秒.①当 秒时,OB平分 此时 ;
②当三角板OAB旋转至图2的位置,此时 与 有怎样的数量关系?请说明理由;
(2)、如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒 的速度逆时针旋转,当OB旋转至射线OM上时同时停止.①当t为何值时,OB平分 ?
②直接写出在旋转过程中, 与 之间的数量关系.
24. 已知线段 ,延长线段AB到C,使得 ,点D是线段AC的中点,求线段BD的长.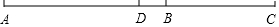 25. 如图①是由一些大小相同的小正方体组合成的简单几何体.(1)、请在图 的方格纸中分别画出它的主视图、左视图和俯视图.
25. 如图①是由一些大小相同的小正方体组合成的简单几何体.(1)、请在图 的方格纸中分别画出它的主视图、左视图和俯视图.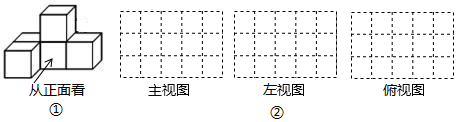 (2)、保持小正方体的个数不变,只改变小正方体的位置,搭一个不同于上图的几何体,使得它的俯视图和左视图与你在方格纸中所画的一致,还有种不同的搭法.26. 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
(2)、保持小正方体的个数不变,只改变小正方体的位置,搭一个不同于上图的几何体,使得它的俯视图和左视图与你在方格纸中所画的一致,还有种不同的搭法.26. 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.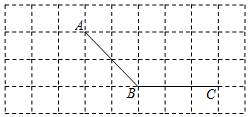 (1)、①过点C画线段AB的平行线CD;
(1)、①过点C画线段AB的平行线CD;②过点A画线段BC的垂线,垂足为E;
③过点A画线段AB的垂线,交线段CB的延长线于点F;
(2)、线段AE的长度是点到直线的距离;(3)、线段AE、BF、AF的大小关系是 用“ ”连接