江苏省南京市鼓楼区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 相反数的倒数是( )A、 B、 C、5 D、2. 习近平同志在十九大报告中指出:农业农村农民问题是关系到国计民生的根本性问题,我国现有农村人口约为589 730 000人,将589 730 000用科学记数法表示为( )A、589 73×104 B、589.73×106 C、5.8973×108 D、0.58973×1083. 下列计算正确的是( )A、 B、 C、3x﹣2x=1 D、4. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )A、
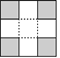 B、
B、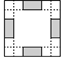 C、
C、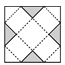 D、
D、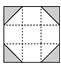 5. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α=∠β的图形有( )
5. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α=∠β的图形有( ) A、1个 B、2个 C、3个 D、4个6. 找出以如图形变化的规律,则第2019个图形中黑色正方形的数量是
A、1个 B、2个 C、3个 D、4个6. 找出以如图形变化的规律,则第2019个图形中黑色正方形的数量是 A、2019 B、3027 C、3028 D、3029
A、2019 B、3027 C、3028 D、3029二、填空题
-
7. 南京市2019年元旦的最低气温为 ,最高气温为 ,这一天的最高气温比最低气温高8. 若∠1=35°21′,则∠1的余角是 .9. 在 、 , 、 , 、 中,是无理数的为.10. 下列三个现象:
用两个钉子就可以把一根木条固定在墙上; 从A地到B地架设电线,只要尽可能沿着线段AB架设,就能节省材料; 植树时,只要定出两棵树的位置,就能使同一行树在一条直线上.其中可用“两点确定一条直线”来解释的现象有 填序号
11. 关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是 .12. 如果 ,那么代数式 的值为.13. 某校七年级学生乘车去郊外秋游,如果每辆汽车坐45人,那么有16人坐不上汽车;如果每辆汽车坐50人,那么有一辆汽车空出9个座位,有x辆汽车,则根据题意可列出方程为.14. 小明父亲拟用不锈钢制造一个上部是一个长方形,下部是一个正方形的窗户,相关数据 单位:米 如图所示,则制造这个窗户所需不锈钢的总长是米 15. 如图,一个长方体的表面展开图中四边形ABCD是正方形 正方形的四个角都是直角、四条边都相等 ,则根据图中数据可得原长方体的体积是 .
15. 如图,一个长方体的表面展开图中四边形ABCD是正方形 正方形的四个角都是直角、四条边都相等 ,则根据图中数据可得原长方体的体积是 . 16. 已知线段 ,在直线AB上取一点P,恰好使 ,点Q为线段PB的中点,则AQ的长为.
16. 已知线段 ,在直线AB上取一点P,恰好使 ,点Q为线段PB的中点,则AQ的长为.三、解答题
-
17. 计算:(1)、(2)、18. 解方程(1)、解方程:(2)、解方程:19. 先化简,再求值:求 的值,其中 , .20. 如图,点C是线段AB上的一点,M是AB的中点,N是CB的中点.
 (1)、若AB=13,CB=5,求MN的长度;(2)、若AC=6,求MN的长度。21. 一项工程,甲单独做需要10天完成,乙单独做需要15天完成.(1)、甲的工作效率是;乙的工作效率是.(2)、两人合作4天后,剩下的部分由乙单独做,则乙还需几天完成?22. 利用直尺画图
(1)、若AB=13,CB=5,求MN的长度;(2)、若AC=6,求MN的长度。21. 一项工程,甲单独做需要10天完成,乙单独做需要15天完成.(1)、甲的工作效率是;乙的工作效率是.(2)、两人合作4天后,剩下的部分由乙单独做,则乙还需几天完成?22. 利用直尺画图 (1)、利用图(1)中的网格,过P点画直线AB的平行线和垂线.(2)、把图(2)网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形.(3)、如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于.23. 按要求完成下列视图问题, 其中小正方体的棱长为
(1)、利用图(1)中的网格,过P点画直线AB的平行线和垂线.(2)、把图(2)网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形.(3)、如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于.23. 按要求完成下列视图问题, 其中小正方体的棱长为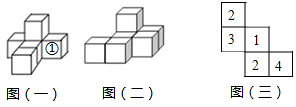 (1)、如图 一 ,它是由六个同样大小的正方体摆成的几何体 将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(1)、如图 一 ,它是由六个同样大小的正方体摆成的几何体 将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?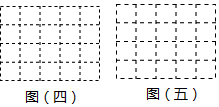 (2)、如图 二 ,请你借助虚线网格 图四 画出该几何体的俯视图,该几何体的体积为.(3)、如图 三 ,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格 图五 画出该几何体的主视图.24. 如图所示,已知点O是直线AB上的一点, ,OF是 的平分线 点C与点E、F在直线AB的两旁,
(2)、如图 二 ,请你借助虚线网格 图四 画出该几何体的俯视图,该几何体的体积为.(3)、如图 三 ,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格 图五 画出该几何体的主视图.24. 如图所示,已知点O是直线AB上的一点, ,OF是 的平分线 点C与点E、F在直线AB的两旁, (1)、若 ,求 ;(2)、若 ,求 ,请说明理由.25. 我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=﹣4的解为x=﹣2,而﹣2=﹣4+2,则方程2x=﹣4为“和解方程”.
(1)、若 ,求 ;(2)、若 ,求 ,请说明理由.25. 我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=﹣4的解为x=﹣2,而﹣2=﹣4+2,则方程2x=﹣4为“和解方程”.请根据上述规定解答下列问题:
(1)、已知关于x的一元一次方程3x=m是“和解方程”,求m的值;(2)、已知关于x的一元一次方程﹣2x=mn+n是“和解方程”,并且它的解是x=n,求m,n的值.26. 我们知道,在数轴上,表示数 表示的点到原点的距离,这是绝对值的几何意义,进一步地,如果数轴上两个点A、B,分别对应数a,b,那么A、B两点间的距离为:如图,点A在数轴上对应的数为a,点B对应的数为b,且a,b满足:
 (1)、求a,b的值;(2)、求线段AB的长;(3)、如图①,点C在数轴上对应的数为x,且是方程 的解,在数轴上是否存在点M使 ?若存在,求出点M对应的数;若不存在,说明理由.(4)、如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断 的值是不变的还是变化的,如果不变请直接写出其值,如果是变化的请说明理由.
(1)、求a,b的值;(2)、求线段AB的长;(3)、如图①,点C在数轴上对应的数为x,且是方程 的解,在数轴上是否存在点M使 ?若存在,求出点M对应的数;若不存在,说明理由.(4)、如图②,若N点是B点右侧一点,NA的中点为Q,P为NB的三等分点且靠近于B点,当N在B的右侧运动时,请直接判断 的值是不变的还是变化的,如果不变请直接写出其值,如果是变化的请说明理由.