江苏南京市秦淮区四校联考2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 比﹣1小2的数是( )A、3 B、1 C、﹣2 D、﹣32. 下列各式中运算正确的是( )A、4m-m=3 B、xy-2xy=-xy C、2x+3y=5xy D、a2b-ab2=03. 下列等式变形正确的是( ).A、如果mx=my,那么x=y B、如果︱x︱=︱y︱,那么x=y C、如果- x=8,那么x=-4 D、如果x-2=y-2,那么x=y4. 现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释图中这一现象,其原因为( ).
 A、两点之间线段的长度,叫做这两点之间的距离 B、过一点有无数条直线 C、两点之间线段最短 D、两点确定一条直线5. 下列各组数中,结果相等的是( ).A、+32与+23 B、-23 与(-2)3 C、-32与(-3)2 D、|-3|3与(-3)36. 若直线l上一点P和直线l外一点Q的距离为8 cm,则点Q到直线l的距离是( )A、等于8 cm B、小于或等于8 cm C、大于8 cm D、以上三种都有可能7. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A、两点之间线段的长度,叫做这两点之间的距离 B、过一点有无数条直线 C、两点之间线段最短 D、两点确定一条直线5. 下列各组数中,结果相等的是( ).A、+32与+23 B、-23 与(-2)3 C、-32与(-3)2 D、|-3|3与(-3)36. 若直线l上一点P和直线l外一点Q的距离为8 cm,则点Q到直线l的距离是( )A、等于8 cm B、小于或等于8 cm C、大于8 cm D、以上三种都有可能7. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )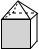 A、
A、 B、
B、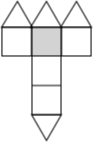 C、
C、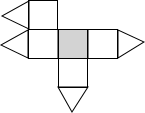 D、
D、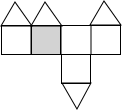 8. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,通过观察,用你所发现的规律确定22011的个位数字是( )A、2 B、4 C、6 D、8
8. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,通过观察,用你所发现的规律确定22011的个位数字是( )A、2 B、4 C、6 D、8二、填空题
-
9. 的倒数是;10. “社会主义核心价值观”要求我们牢记心间,小明在“百度”搜索“社会主义核心价值观”,找到相关结果约为 个,数据 用科学记数法表示为.11. 比较大小: .12. 若5x6y2m与-3xn+9y6和是单项式,那么n-m的值为 .13. 若x=-1是关于x的方程2x+a=1的解,则a的值为.14. 若∠α与∠β是对顶角,∠α的补角是35°,则∠β的度数为.15. 如图是某正方体的展开图,则原正方体相对两个面上的数字和的最大值是.
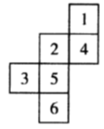 16. 一件衬衫先按成本加价60元标价,再以8折出售,仍可获利24元,这件衬衫的成本是元.17. 在同一平面内,∠BOC=50°,OA⊥OB,OD平分∠AOC,则∠BOD的度数是.18. 三个互不相等的有理数,既可以表示为1、a+b、a的形式,也可以表示为0、 、b的形式,则字母a表示的有理数是.
16. 一件衬衫先按成本加价60元标价,再以8折出售,仍可获利24元,这件衬衫的成本是元.17. 在同一平面内,∠BOC=50°,OA⊥OB,OD平分∠AOC,则∠BOD的度数是.18. 三个互不相等的有理数,既可以表示为1、a+b、a的形式,也可以表示为0、 、b的形式,则字母a表示的有理数是.三、解答题
-
19. 计算:(1)、( + - )÷(- );(2)、-14-(1+0.5)× ÷(-4)2.20. 已知3a﹣7b=﹣3,求代数式2(2a+b﹣1)+5(a﹣4b)﹣3b的值.21. 解方程:(1)、4(x-1)-3=7(2)、 - =1.22. 如图,A、B、C,依次为直线L上三点,M为AB的中点,N为MC的中点,且AB=6cm,NC=8cm,求BC的长。
 23. 如图是由10个同样大小的小正方体搭成的物体,(1)、请分别画出它的主视图和俯视图.(2)、在主视图和俯视图不变的情况下,你认为最多还可以添加个小正方体.
23. 如图是由10个同样大小的小正方体搭成的物体,(1)、请分别画出它的主视图和俯视图.(2)、在主视图和俯视图不变的情况下,你认为最多还可以添加个小正方体. 24. 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
24. 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上. (1)、①过点C画线段AB的平行线CD;
(1)、①过点C画线段AB的平行线CD;②过点A画线段BC的垂线段,垂足为G;
③过点A画线段AB的垂线,交BC于点H;
(2)、线段的长度是点H到直线AB的距离;(3)、在以上所画的图中与∠B相等的角是.25. 甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?26. 定义☆运算,观察下列运算:(+5)☆(+14) =+19 (-13)☆(-7) =+20,
(-2)☆(+15) =-17 (+18)☆(-7) =-25,
0☆(-19) =+19 (+13)☆0 =+13.
(1)、请你认真思考上述运算,归纳☆运算的法则:两数进行☆运算时,同号 , 异号.
特别地,0和任何数进行☆运算,或任何数和0进行☆运算,.
(2)、计算:(+17) ☆[0 ☆(-16)] = .(3)、若2×(2☆a)-1=3a,求a的值.27. 如图 1,射线 OC在∠AOB的内部,图中共有 3个角:∠AOB、∠AOC 和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线 OC是∠AOB的奇妙线.
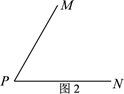
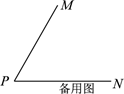 (1)、一个角的角平分线这个角的奇妙线.(填是或不是);(2)、如图 2,若∠MPN=60°,射线 PQ绕点 P从 PN位置开始,以每秒 10°的速度逆时针旋转,当∠QPN首次等于 180°时停止旋转,设旋转的时间为 t(s).
(1)、一个角的角平分线这个角的奇妙线.(填是或不是);(2)、如图 2,若∠MPN=60°,射线 PQ绕点 P从 PN位置开始,以每秒 10°的速度逆时针旋转,当∠QPN首次等于 180°时停止旋转,设旋转的时间为 t(s).①当 t为何值时,射线 PM是∠QPN 的奇妙线?
②若射线 PM 同时绕点 P以每秒 5°的速度逆时针旋转,并与 PQ同时停止旋转.请求出当射线 PQ是∠MPN的奇妙线时 t的值.