江苏省扬州市宝应县2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 已知⊙O的直径为10,OA=6,则点A在( )A、⊙O上 B、⊙O外 C、⊙O内 D、无法确定2. 如图,线段AD、CB相交于点O,连结AB、CD,∠A=∠C,则下列结论正确的是( )
 A、 B、 C、 D、3. 二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
A、 B、 C、 D、3. 二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( ) A、函数有最小值 B、对称轴是直线x= C、当x< ,y随x的增大而减小 D、当 -1 < x < 2时,y>04. 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )
A、函数有最小值 B、对称轴是直线x= C、当x< ,y随x的增大而减小 D、当 -1 < x < 2时,y>04. 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )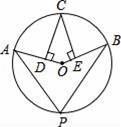 A、140° B、70° C、60° D、40°5. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )A、15° B、30° C、45° D、60°6. 如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A、140° B、70° C、60° D、40°5. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )A、15° B、30° C、45° D、60°6. 如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )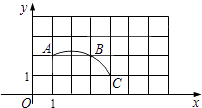 A、点(0,3) B、点(2,3) C、点(5,1) D、点(6,1)7. 二次函数y=ax2+bx+c的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③2a﹣b=0;④abc>0,其中正确结论的个数是( )
A、点(0,3) B、点(2,3) C、点(5,1) D、点(6,1)7. 二次函数y=ax2+bx+c的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③2a﹣b=0;④abc>0,其中正确结论的个数是( )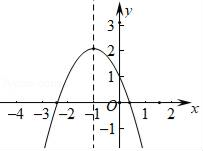 A、4个 B、3个 C、2个 D、1个8. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=6,AB=10,则DE的长为( )
A、4个 B、3个 C、2个 D、1个8. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=6,AB=10,则DE的长为( )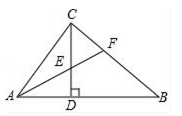 A、 B、3 C、 D、
A、 B、3 C、 D、二、填空题
-
9. 在比例尺为1:50000的宝应交通地图上,某条道路的实际长度为5km,则这条道路在地图上的长度为cm10. 已知线段AB=10cm,点P是线段AB的黄金分割点,且PA>PB,则PA=cm.(精确到0.1)11. 若一元二次方程 的两个实数根分别是3、 ,则 =.
12. 如图,以点O为位似中心,将四边形ABCD按1:2放大得到四边形A′B′C′D′,则四边形ABCD与四边形A′B′C′D′的面积比是.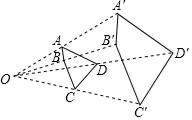 13. 在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b,c,a=3,c=5,则tanB=.14. 如图所示,身高1.6m的小华站在距路灯杆5m的C点处,测得他在灯光下的影长CD为3.2m,则路灯AB的高度为m.
13. 在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b,c,a=3,c=5,则tanB=.14. 如图所示,身高1.6m的小华站在距路灯杆5m的C点处,测得他在灯光下的影长CD为3.2m,则路灯AB的高度为m.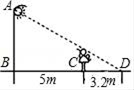 15. 如图,△ABC中,点O是重心,过点O的两条线段BE⊥AD.若BD=10,BO=8,则AO的长为.
15. 如图,△ABC中,点O是重心,过点O的两条线段BE⊥AD.若BD=10,BO=8,则AO的长为.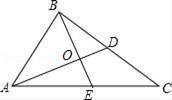 16. 如图,已知▱ABCD中,点E在CD上, ,BE交对角线AC于点F.则 =.
16. 如图,已知▱ABCD中,点E在CD上, ,BE交对角线AC于点F.则 =. 17. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为.
17. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为.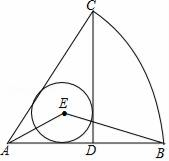
三、解答题
-
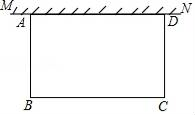
18. 解方程或计算化简:(1)、解方程:x2+6x=0(2)、计算化简:( )﹣2﹣8cos60°﹣( )019. 如图,在足够大的空地上有一段长为20米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了40米木栏,所围成的矩形菜园的面积为150平方米,求矩形菜园的边长BC和AB.
 20. 为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如表:
20. 为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩记录如表:射击次序(次)
1
2
3
4
5
6
7
8
9
10
甲的成绩(环)
8
9
7
9
8
6
7
a
10
8
乙的成绩(环)
6
7
9
7
9
10
8
7
7
10
(1)、经计算甲和乙的平均成绩是8(环),请求出表中的a=;(2)、甲成绩的中位数是环,乙成绩的众数是环;(3)、若甲成绩的方差是1.2,请求出乙成绩的方差,判断甲、乙两人谁的成绩更为稳定?21. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)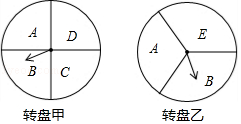 (1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.22. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,以点D为圆心,DC为半径作圆.
(1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.22. 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,以点D为圆心,DC为半径作圆.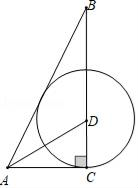 (1)、试判断直线AB与⊙D的位置关系,并说明理由;(2)、若CD= BD,求∠B.23. 已知:二次函数y1=ax2+bx+c(a≠0)的对称轴为过点(2,0)且平行于y轴的一条直线,与直线y2=kx+b(k≠0)交于点A(1,0)、B(4,9).
(1)、试判断直线AB与⊙D的位置关系,并说明理由;(2)、若CD= BD,求∠B.23. 已知:二次函数y1=ax2+bx+c(a≠0)的对称轴为过点(2,0)且平行于y轴的一条直线,与直线y2=kx+b(k≠0)交于点A(1,0)、B(4,9).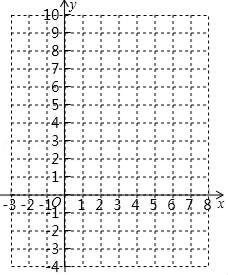 (1)、求这个二次函数解析式;(2)、在所给的平面直角坐标系中直接画出二次函数的图象(不要求列表),并根据图象直接写出y1≤y2时,x的取值范围.24. 如图,点E、F分别是正方形ABCD的边BC、CD上的动点,连结AE、EF.
(1)、求这个二次函数解析式;(2)、在所给的平面直角坐标系中直接画出二次函数的图象(不要求列表),并根据图象直接写出y1≤y2时,x的取值范围.24. 如图,点E、F分别是正方形ABCD的边BC、CD上的动点,连结AE、EF. (1)、若点E是BC的中点,CF:FD=1:3,求证:△ABE∽△ECF;(2)、若AE⊥EF,设正方形的边长为6,BE=x,CF=y.当x取什么值时,y有最大值?并求出这个最大值.25. 小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
(1)、若点E是BC的中点,CF:FD=1:3,求证:△ABE∽△ECF;(2)、若AE⊥EF,设正方形的边长为6,BE=x,CF=y.当x取什么值时,y有最大值?并求出这个最大值.25. 小明家所在居民楼的对面有一座大厦AB=74米,为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.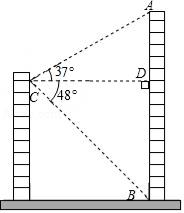 (1)、求小明家所在居民楼与大厦的距离CD的长度.(参考数据:sin37°≈ ,tan37°≈ ,sin48°≈ ,tan48°≈ )(2)、冬季,在阳光的照射下测得一根1m长的竹竿在地面的影长是1.6m,试问此时太阳光是否能直射到小明家?请通过计算说明.26. 如图,在Rt△AOB中,∠AOB=90°,tanB= ,OB=8.
(1)、求小明家所在居民楼与大厦的距离CD的长度.(参考数据:sin37°≈ ,tan37°≈ ,sin48°≈ ,tan48°≈ )(2)、冬季,在阳光的照射下测得一根1m长的竹竿在地面的影长是1.6m,试问此时太阳光是否能直射到小明家?请通过计算说明.26. 如图,在Rt△AOB中,∠AOB=90°,tanB= ,OB=8.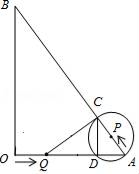 (1)、求OA、AB的长;(2)、点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD,QC.
(1)、求OA、AB的长;(2)、点Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD,QC.①当t为何值时,点Q与点D重合?
②若⊙P与线段QC只有一个公共点,求t的取值范围.
27. 已知,如图1,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为C与x轴交于A、B两点(点A在点B左侧),点C、B关于过点A的直线l:y=kx+ 对称.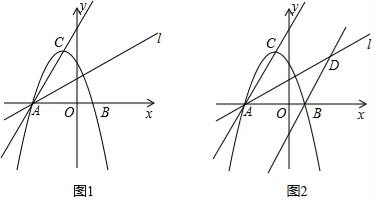 (1)、求A、B两点坐标及直线l的解析式;(2)、求二次函数解析式;(3)、如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l上的两个动点,连接CN,MM、MD,求CN+NM+MD的最小值.
(1)、求A、B两点坐标及直线l的解析式;(2)、求二次函数解析式;(3)、如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l上的两个动点,连接CN,MM、MD,求CN+NM+MD的最小值.