江苏省宿迁市泗阳县2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 一个布袋里装有6个只有颜色可以不同的球，其中2个红球，4个白球．从布袋里任意摸出1个球，则摸出的球是红球的概率为（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{6}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 已知一元二次x²+x﹣2＝0的一个根是﹣2，则该方程的另一个根是（）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
3. 如图，AB是⊙O的直径，BC是⊙O的弦，已知∠AOC＝80°，则∠ABC的度数为（）

A、20° B、30° C、40° D、50°

查看试题解析
4. 二次函数y＝（x﹣1）²﹣2图象的对称轴是（）

A、直线x＝1 B、直线x＝﹣1 C、直线x＝2 D、直线x＝﹣2

查看试题解析
5. 一组数据按从大到小排列为2，4，8，x，10，14．若这组数据的中位数为9，则这组数据的众数为( )

A、6 B、8 C、9 D、10

查看试题解析
6. 连续两个整数的乘积为12，则这两个整数中较小的一个是（）

A、3 B、﹣4 C、﹣3或4 D、﹣4或3

查看试题解析
7. 如图，圆锥的底面半径为2，母线长为6，则侧面积为（）

A、4π B、6π C、12π D、16π

查看试题解析
8. 一张面积为240的长方形彩纸，长比宽大8，设它的宽为x，可列方程（）

A、8x＝240 B、x（x﹣8）＝240 C、x（x+8）＝240 D、8（8+x）＝240

查看试题解析
9. 将六个全等的等边三角形沿中位线剪开，得到六个全等的等腰梯形，将六个等腰梯形按如图所示围成一个圆的内接正六边形和一个小正六边形，若小正六边形的面积为6，则圆的内接六边形的面积为（）

A、24 B、18 C、12 D、6

查看试题解析
10. 已知二次函数y＝ax²+bx+c中，自变量x与函数y之间的部分对应值如表：

x

…

0

1

2

3

…

y

…

﹣1

2

3

2

…

在该函数的图象上有A（x₁ ， y₁）和B（x₂ ， y₂）两点，且﹣1＜x₁＜0，3＜x₂＜4，y₁与y₂的大小关系正确的是（）

A、y₁≥y₂ B、y₁＞y₂ C、y₁≤y₂ D、y₁＜y₂

查看试题解析

二、填空题

11. 数据﹣5，6，4，0，1，7，5的极差为.

查看试题解析
12. 如图，AB与⊙O相切于点B，AO延长线交⊙O于C点，若AC＝8，OB＝3，则AB＝.

查看试题解析
13. 一元二次方程x²﹣2x＝0的两根分别为x₁和x₂ ，则x₁x₂为.

查看试题解析
14. 小明向如图所示的正方形木板投掷1枚飞镖，若飞镖击中图中每一个小正方形是等可能的，则击中阴影部分的概率是.

查看试题解析
15. 二次函数y＝x²﹣3x+c的图象与x轴有且只有一个交点，c＝.

查看试题解析
16. 把一个正多边形绕它的中心旋转40°后能与原来的位置重合，则这个多边形的边数至少是.

查看试题解析
17. 若抛物线C₁：y＝x²+mx+2与抛物线C₂：y＝x²﹣3x+n关于y轴对称，则m+n＝.

查看试题解析
18. 我们发现：若AD是△ABC的中线，则有AB²+AC²＝2（AD²+BD²），请利用结论解决问题：如图，在矩形ABCD中，已知AB＝20，AD＝12，E是DC中点，点P在以AB为直径的半圆上运动，则CP²+EP²的最小值是.

查看试题解析

三、解答题

19. 解下列一元二次方程：

(1)、x²﹣4x+3＝0

(2)、（2x﹣1）²﹣x²＝0

查看试题解析
20. 如图，AD是⊙O的弦，AB经过圆心O交⊙O于点C，∠A＝∠B＝30°，连接BD.求证：BD是⊙O的切线.

查看试题解析
21. 抛物线y＝ax²﹣2x+c与x轴交点坐标为A（﹣1，0），B（3，0），与y轴交点坐标为C（0，n）.

(1)、求抛物线的解析式；

(2)、计算△ABC的面积.

查看试题解析
22. 某篮球队在一次联赛中共进行了10场比赛，已知这10场比赛的平均得分为48分，且前9场比赛的得分依次为：57，51，45，51，44，46，45，42，48.

(1)、求第10场比赛的得分；

(2)、直接写出这10场比赛的中位数，众数和方差.
方差公式：s²＝ $\frac{1}{n}$ [（x₁﹣ $\bar{x}$ ）²+（x₂﹣ $\bar{x}$ ）²+…+（x_n﹣ $\bar{x}$ ）²]

查看试题解析
23. 如图，在矩形ABCD中，AB＝16cm，BC＝6cm，点P从A点出发沿AB以5cm/s的速度向点B移动，一直到达点B为止；同时，点Q从C点出发沿CD以3cm/s的速度向点D移动，经过多长时间P、Q两点之间的距离为10cm？

查看试题解析
24. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：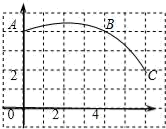

(1)、请在图中确定该圆弧所在圆心D点的位置，D点坐标为；

(2)、连接AD、CD，则⊙D的半径为；扇形DAC的圆心角度数为；

(3)、若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径.

查看试题解析
25. 某商场以每件40元的价格购进一种服装，由试销知，每天的销售量t（件）与每件的销售价x（元）之间的函数关系为t＝180﹣3x.

(1)、试写出每天销售这种服装的毛利润y（元）与每件销售价x（元）之间的函数表达式（毛利润＝销售价﹣进货价）；

(2)、每件销售价为多少元，才能使每天的毛利润最大？最大毛利润是多少？

查看试题解析
26. P是以AB为直径的半圆上一动点（P与A、B不重合），O为圆心，CO⊥AP，OC、BC与AP分别相交于D、E两点，AB＝12.

(1)、若∠ABC＝35°，求∠PAB的度数；

(2)、若AP平分线段BC，求弦AP的长度；

(3)、是否存在点P，使△PBC的面积为整数，如果存在，这样的P点有几个？（直接写出结果，不需写出解题过程.）

查看试题解析
27. 如图

(1)、如图1，若点A坐标为（x₁ ， y₁），点B坐标为（x₂ ， y₂），作AD⊥x轴于点D，BE⊥y轴于点E，AD与BE相交于点C，则有AC＝|y₁﹣y₂|，BC＝|x₁﹣x₂|，所以，A、B两点间的距离为AB＝ $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ .
根据结论，若M、N两点坐标分别为（1，4）、（5，1），则MN＝（直接写出结果）.

(2)、如图2，直线y＝kx+1与y轴相交于点D，与抛物线y＝ $\frac{1}{4}$ x²相交于A，B两点，A点坐标为（4，a），过点A作y轴的垂线交y轴于点C，E是AC中点，点P是第一象限内直线AB下方抛物线上一动点，连接PE、PD、ED；
①a＝， k＝， AD＝（直接写出结果）.

②若△DEP是以DE为底的等腰三角形，求点P的横坐标；

③求四边形CDPE的周长的最小值.

查看试题解析

x	…	0	1	2	3	…
y	…	﹣1	2	3	2	…