江苏省无锡市滨湖区2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

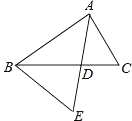
1. 方程x²＝x的根是（）

A、x＝0 B、x＝1 C、x＝0 或x＝1 D、x＝0 或x＝﹣1

查看试题解析
2. 若方程(x﹣4)²＝a有实数解，则a的取值范围是（）

A、a≤0 B、a≥0 C、a＞0 D、a＜0

查看试题解析
3. 若直线l与半径为6的⊙O相交，则圆心O到直线l的距离d为（）

A、d＜6 B、d＝6 C、d＞6 D、d≤6

查看试题解析
4. 若要得到函数y＝（x+1）²+2的图象，只需将函数y＝x²的图象（）

A、先向右平移1个单位长度，再向上平移2个单位长度 B、先向左平移1个单位长度，再向上平移2个单位长度 C、先向左平移1个单位长度，再向下平移2个单位长度 D、先向右平移1个单位长度，再向下平移2个单位长度

查看试题解析
5. 抛物线y＝﹣2(x﹣1)²﹣3与y轴交点的纵坐标为（）

A、﹣5 B、﹣4 C、﹣3 D、﹣1

查看试题解析
6. 用半径为5的半圆围成一个圆锥的侧面，则该圆锥的底面半径等于（）

A、3 B、5 C、 $\frac{3}{2}$ D、 $\frac{5}{2}$

查看试题解析
7. 若等腰△ABC内接于⊙O，AB＝AC，∠BOC＝100°，则△ABC底角的度数为（）

A、65° B、25° C、65°或25° D、65°或30°

查看试题解析
8. 如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（）

A、 $\frac{20}{3}$ B、 $\frac{15}{4}$ C、 $\frac{16}{3}$ D、 $\frac{17}{4}$

查看试题解析
9. 如图，直线y＝ $\frac{1}{2}$ x＋1与x轴、y轴分别相交于A、B两点，P是该直线上的任一点，过点D（3，0）向以P为圆心， $\frac{1}{2}$ AB为半径的⊙P作两条切线，切点分别为E、F，则四边形PEDF面积的最小值为（）

A、 $\frac{5}{4} \sqrt{3}$ B、 $\sqrt{5}$ C、 $2 \sqrt{5}$ D、 $\frac{5}{2} \sqrt{3}$

查看试题解析

二、填空题

10. 若3是方程x²﹣2x+c＝0的一个根，则c的值为.

查看试题解析
11. 若 $\frac{a}{b} = \frac{3}{5}$ ，则 $\frac{a + b}{b}$ ＝.

查看试题解析
12. 抛物线y＝x²﹣2x﹣5的顶点坐标是.

查看试题解析
13. 如图，交警统计了某个时段在一个路口来往车辆的车速(单位：千米/时)情况，则该时段内来往车辆的平均速度是千米/时.

查看试题解析
14. 如图，⊙O的半径是3，点A、B、C在⊙O上，若∠ACB＝40°，则弧AB的长为.

查看试题解析
15. 半径相等的圆内接正三角形与正方形的边长之比为.

查看试题解析
16. 如图，圆内接四边形ABCD的边AB过圆心O，过点C的切线与边AD所在直线垂直于点M，若∠ABC＝65°，则∠ACD＝°.

查看试题解析
17. 记抛物线C₁：y＝(x﹣2)²+3的顶点为A，抛物线C₂：y＝ax²+1(a＜0)顶点是点B，且与x轴的正半轴交于点 C.当△ABC是直角三角形时，抛物线C₂的解析式为.

查看试题解析

三、解答题

18.

(1)、计算： $\sqrt{8} - | - \sqrt{2} | + {(- \frac{1}{2})}^{0}$ ；

(2)、解方程：x²﹣4x+1＝0.

查看试题解析
19. 如图，在平面直角坐标系中，每个小方格都是边长为1个单位长度的小正方形，点A、B、C都是格点(每个小方格的顶点叫格点)，其中A(5，6)，B(3，6)，C(2，7).

(1)、已知△ABC与△DEF(点D、E、F都是格点)成位似图形，则位似中心M的坐标是；

(2)、△ABC外接圆半径是；

(3)、请在网格图中画一个格点△A₁B₁C₁ ，使△A₁B₁C₁∽△DEF，且相似比为1：2.

查看试题解析
20. 近年来网约车十分流行，初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查，司机月收入(单位：千元)如图所示：

根据以上信息，整理分析数据如下：

平均月收入/千元
中位数/千元
众数/千元
方差/千元²
“美团”
①______
6
6
1.2
“滴滴”
6
②____
4
③_____

(1)、完成表格填空；

(2)、若从两家公司中选择一家做网约车司机，你会选哪家公司，并说明理由.

查看试题解析
21. 甲、乙、丙三人进行乒乓球比赛.他们通过摸球的方式决定首场比赛的两个选手：在一个不透明的口袋中放入两个红球和一个白球，这些球除颜色外其他都相同，将它们搅匀，三人从中各摸出一个球，摸到红球的两人即为首场比赛选手.求甲、丙两人成为比赛选手的概率.(请用画树状图或列表等方法写出分析过程并给出结果.)

查看试题解析
22. 如图，已知AB∥CD，AC与BD相交于点E，∠ABE＝∠ACB.

(1)、求证：△ABE∽△ACB；

(2)、如果AB＝6，AE＝4，求CD的长.

查看试题解析
23. 如图1，已知四边形ABCD内接于⊙O，AC为⊙O的直径，AD＝DB，AC与BD交于点E，且AE＝BC.

(1)、求证：AB＝CB；

(2)、如图2，△ABC绕点C逆时针旋转35°得到△FGC，点A经过的路径为弧AF，若AC＝4，求图中阴影部分的面积.

查看试题解析
24. 某商场要经营一种新上市的文具，进价为20元/件.试营销阶段发现：当销售单价为25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件.

(1)、写出每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；并求当x为多少时，w有最大值，最大值是多少？

(2)、商场的营销部结合上述情况，提出了甲、乙两种营销方案：方案甲：该文具的销售单价高于进价且不超过30元；方案乙：每天销售量不少于10件，且每件文具的利润至少为25元.请比较哪种方案的最大利润更高，并说明理由.

查看试题解析
25. 如图，在矩形ABCD中，已知AB＝6，BC＝8，动点P从点D出发，沿DA的方向运动到点A，每秒1个单位，同时点Q从点B出发，沿BD的方向运动到点D，每秒5个单位.当某一个点到达终点时，整个运动就停止.设运动时间为t(秒).

(1)、填空：当t＝时，PQ∥AB；

(2)、设△PCQ的面积为S，求S关于t的函数表达式；

(3)、当直线CQ与以点P为圆心，PQ为半径的圆相切时，求t的值.

查看试题解析
26. 如图，直线y＝ $\frac{1}{2}$ x+2分别与x轴、y轴交于C、D两点，二次函数y＝﹣x²+bx+c的图象经过点D，与直线相交于点E，且CD：DE＝4：3.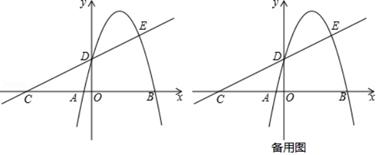

(1)、求点E的坐标和二次函数表达式；

(2)、过点D的直线交x轴于点M.
①当DM与x轴的夹角等于2∠DCO时，请直接写出点M的坐标；

②当DM⊥CD时，过抛物线上一动点P(不与点D、E重合)，作DM的平行线交直线CD于点Q，若以D、M、P、Q为顶点的四边形是平行四边形，求点P的横坐标.

查看试题解析

	平均月收入/千元	中位数/千元	众数/千元	方差/千元²
“美团”	①______	6	6	1.2
“滴滴”	6	②____	4	③_____