江苏省苏州市张家港市2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
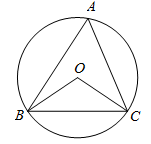
1. 抛物线 与 轴的交点坐标为( )A、(3 ,0) B、(0 ,3) C、(0, ) D、( ,0)2. 已知 ,则 的值是( )A、 B、 C、 D、﹣3. 如图,⊙O是△ABC的外接圆,∠A= ,则∠BOC的大小为( )
 A、40° B、30° C、80° D、100°4. 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC的长是( )
A、40° B、30° C、80° D、100°4. 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC的长是( ) A、2 B、8 C、2 D、45. 若要得到函数y=(x+1)2+2的图象,只需将函数y=x2的图象( )A、先向右平移1个单位长度,再向上平移2个单位长度 B、先向左平移1个单位长度,再向上平移2个单位长度 C、先向左平移1个单位长度,再向下平移2个单位长度 D、先向右平移1个单位长度,再向下平移2个单位长度6. 如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为( )
A、2 B、8 C、2 D、45. 若要得到函数y=(x+1)2+2的图象,只需将函数y=x2的图象( )A、先向右平移1个单位长度,再向上平移2个单位长度 B、先向左平移1个单位长度,再向上平移2个单位长度 C、先向左平移1个单位长度,再向下平移2个单位长度 D、先向右平移1个单位长度,再向下平移2个单位长度6. 如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=4,BD=8,AE=2,则CE的长为( ) A、3 B、 C、4 D、7. △DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )
A、3 B、 C、4 D、7. △DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,若△DEF的面积是2,则△ABC的面积是( )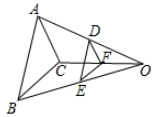 A、2 B、4 C、6 D、88. 如图,港口 在观测站 的正东方向, =4km,某船从港口 出发,沿北偏东 方向航行一段距离后到达 处,此时从观测站 处侧得该船位于北偏东 的方向,则该船与观测站之间的距离(即 的长)为( )
A、2 B、4 C、6 D、88. 如图,港口 在观测站 的正东方向, =4km,某船从港口 出发,沿北偏东 方向航行一段距离后到达 处,此时从观测站 处侧得该船位于北偏东 的方向,则该船与观测站之间的距离(即 的长)为( ) A、 km B、 km C、 km D、 km9. 如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=4 ,CE=8,则⊙O的半径是( )
A、 km B、 km C、 km D、 km9. 如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=4 ,CE=8,则⊙O的半径是( ) A、 B、5 C、6 D、10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )
A、 B、5 C、6 D、10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( )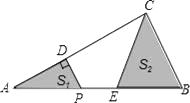 A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小
A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小二、填空题
-
11. 抛物线y=﹣(x﹣4)2+2的最大值为.12. 已知扇形的半径为4㎝,圆心角为120°,则此扇形的弧长是㎝13. 如图,在△ABC中点D,E分别在AB,AC上,DE∥BC,若S△ADE=1,S四边形DBCE=8,则AD:AB=.
 14. 如图, 中, 交 于点 ,则 的长等于.
14. 如图, 中, 交 于点 ,则 的长等于. 15. 如图,在正方形网格中,每个小正方形的边长都是1, 的每个顶点都在格点上,则 =.
15. 如图,在正方形网格中,每个小正方形的边长都是1, 的每个顶点都在格点上,则 =. 16. 如图,双曲线y= 与抛物线y=ax2+bx+c交于点A(x1 , y1),B(x2 , y2),C(x3 , y3),由图象可得不等式组0< +bx+c的解集为.
16. 如图,双曲线y= 与抛物线y=ax2+bx+c交于点A(x1 , y1),B(x2 , y2),C(x3 , y3),由图象可得不等式组0< +bx+c的解集为.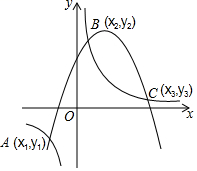 17. 如图, 是⊙ 的直径, 分别与⊙ 相切于点 ,若 ,则图中阴影部分的面积为.
17. 如图, 是⊙ 的直径, 分别与⊙ 相切于点 ,若 ,则图中阴影部分的面积为. 18. 已知抛物线 上部分点的横坐标 与纵坐标 的对应值如下表:
18. 已知抛物线 上部分点的横坐标 与纵坐标 的对应值如下表:
有以下几个结论:①抛物线 的开口向上;②抛物线 的对称轴为直线 ;③方程 的根为0和2;④当 时, 的取值范围是 或 .其中正确的结论是(把你认为正确结论的序号都填上).
三、解答题
-
19. 计算: .20. 已知二次函数的表达式为: ,(1)、利用配方法将表达式化成 的形式;(2)、写出该二次函数图象的对称轴和顶点坐标.21. 在Rt△ABC中,∠C=90°,c=4,a=2 ,解这个直角三角形.22. 如图,AB是⊙O的直径,AC是⊙O的弦,∠ACB的平分线交⊙O于点D,若AB=10,求BD的长.
 23. 如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
23. 如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°. (1)、求证:△ADE∽△BEC.(2)、若AD=1,BC=3,AE=2,求AB的长.24. 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1: .
(1)、求证:△ADE∽△BEC.(2)、若AD=1,BC=3,AE=2,求AB的长.24. 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1: .
(答案均精确到0.1米,参考数据: ≈1.41, ≈2.24, ≈2.45)
(1)、求通道斜面AB的长;(2)、为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.25. 小丽老师家有一片80棵桃树的桃园,现准备多种一些桃树提高桃园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该桃园每棵桃树产桃 (千克)与增种桃树 (棵)之间的函数关系如图所示. (1)、求 与 之间的函数关系式;(2)、在投入成本最低的情况下,增种桃树多少棵时,桃园的总产量可以达到6750千克?(3)、如果增种的桃树 (棵)满足: ,请你帮小丽老师家计算一下,桃园的总产量最少是多少千克,最多又是多少千克?26. 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.
(1)、求 与 之间的函数关系式;(2)、在投入成本最低的情况下,增种桃树多少棵时,桃园的总产量可以达到6750千克?(3)、如果增种的桃树 (棵)满足: ,请你帮小丽老师家计算一下,桃园的总产量最少是多少千克,最多又是多少千克?26. 如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.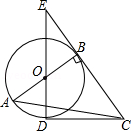 (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE=4,DE=8,求AC的长.27. 如图,直线y=x+c与x轴交于点A(﹣4,0),与y轴交于点C,抛物线y=﹣x2+bx+c经过点A,C.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE=4,DE=8,求AC的长.27. 如图,直线y=x+c与x轴交于点A(﹣4,0),与y轴交于点C,抛物线y=﹣x2+bx+c经过点A,C. (1)、求抛物线的解析式;(2)、已知点P是抛物线上的一个动点,并且点P在第二象限内,过动点P作PE⊥x轴于点E,交线段AC于点D.
(1)、求抛物线的解析式;(2)、已知点P是抛物线上的一个动点,并且点P在第二象限内,过动点P作PE⊥x轴于点E,交线段AC于点D.①如图1,过D作DF⊥y轴于点F,交抛物线于M,N两点(点M位于点N的左侧),连接EF,当线段EF的长度最短时,求点P,M,N的坐标;
②如图2,连接CD,若以C,P,D为顶点的三角形与△ADE相似,求△CPD的面积.
28. 如图1,直线l: 与x轴交于点 ,与y轴交于点B,点C是线段OA上一动点 以点A为圆心,AC长为半径作 交x轴于另一点D,交线段AB于点E,连结OE并延长交 于点F. (1)、求直线l的函数表达式和 的值;(2)、如图2,连结CE,当 时,
(1)、求直线l的函数表达式和 的值;(2)、如图2,连结CE,当 时,①求证: ∽ ;
②求点E的坐标;