江苏省如皋市2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 四个大小相同的正方体搭成的几何体如图所示,其左视图是( ).
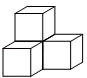 A、
A、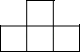 B、
B、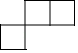 C、
C、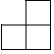 D、
D、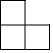 2. 抛物线 顶点坐标是( )A、 B、 C、 D、3. 一个几何体的三视图如图所示,则这个几何体是( )
2. 抛物线 顶点坐标是( )A、 B、 C、 D、3. 一个几何体的三视图如图所示,则这个几何体是( ) A、
A、 B、
B、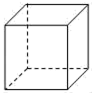 C、
C、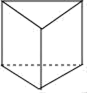 D、
D、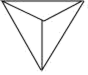 4. 如图,在 的正方形方格图形中,小正方形的顶点称为格点 若 的顶点都在格点上,则 的值等于
4. 如图,在 的正方形方格图形中,小正方形的顶点称为格点 若 的顶点都在格点上,则 的值等于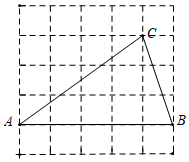 A、 B、 C、 D、5. 如图,在 中,两条中线BE、CD相交于点O,则 :
A、 B、 C、 D、5. 如图,在 中,两条中线BE、CD相交于点O,则 :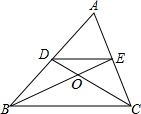 A、1:4 B、2:3 C、1:3 D、1:26. 如图,在平面直角坐标系中, 经过三点 , , ,点D是 上一动点,则点D到弦OB的距离的最大值是
A、1:4 B、2:3 C、1:3 D、1:26. 如图,在平面直角坐标系中, 经过三点 , , ,点D是 上一动点,则点D到弦OB的距离的最大值是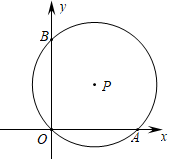 A、6 B、8 C、9 D、107. 点P1(﹣1, ),P2(3, ),P3(5, )均在二次函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 已知点 、 都在反比例函数 的图象上,且 ,则下列结论一定成立的是A、 B、 C、 D、9. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A、6 B、8 C、9 D、107. 点P1(﹣1, ),P2(3, ),P3(5, )均在二次函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 已知点 、 都在反比例函数 的图象上,且 ,则下列结论一定成立的是A、 B、 C、 D、9. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )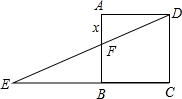 A、
A、 B、
B、 C、
C、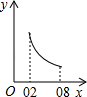 D、
D、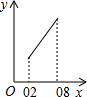 10. 如图,▱ABCD中, , , , 是边AB上的两点,半径为2的 过点A,半径为1的 过点 、E、F分别是边CD, 和 上的动点 则 的最小值等于
10. 如图,▱ABCD中, , , , 是边AB上的两点,半径为2的 过点A,半径为1的 过点 、E、F分别是边CD, 和 上的动点 则 的最小值等于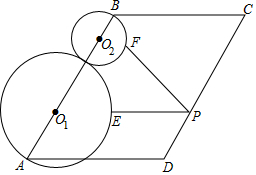 A、 B、6 C、 D、9
A、 B、6 C、 D、9二、填空题
-
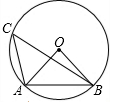
11. 如图,A,B是 上的两点, ,点C在优弧 上,则 度
 12. 已知点A(a,4)、B(﹣2,2)都在双曲线y= 上,则a=.13. 求值: .14. 如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB=m.
12. 已知点A(a,4)、B(﹣2,2)都在双曲线y= 上,则a=.13. 求值: .14. 如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB=m.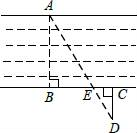 15. 如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积是49,则 的值等于.
15. 如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积是49,则 的值等于.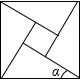 16. 用半径为 ,圆心角为 的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为 .17. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为.
16. 用半径为 ,圆心角为 的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为 .17. 如图,在平面直角坐标系中,每个小方格都是边长为1个单位长度的正方形.已知△AOB与△A1OB1位似中心为原点O,且相似比为3:2,点A,B都在格点上,则点B1的坐标为.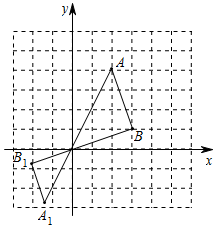 18. 在直角坐标系中,已知直线 经过点 和点 ,抛物线y=ax2-x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是.
18. 在直角坐标系中,已知直线 经过点 和点 ,抛物线y=ax2-x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是.三、解答题
-
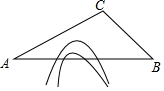
19. 高铁大大缩短了时空距离,改变了人们的出行方式,如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程 已知 , , 公里,求隧道打通后,从A地到B地的路程 结果保留根号 .
 20. 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
20. 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: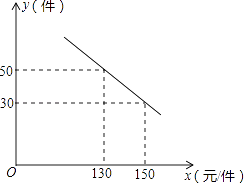 (1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?21. 如图,一次函数 与函数 的图象交于 , 两点, 轴于C, 轴于D
(1)、求出y与x之间的函数关系式;(2)、写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?21. 如图,一次函数 与函数 的图象交于 , 两点, 轴于C, 轴于D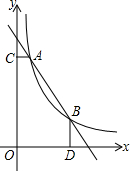 (1)、求k的值;(2)、根据图象直接写出 的x的取值范围;(3)、 是线段AB上的一点,连接PC,PD,若 和 面积相等,求点P坐标.22. 如图, 为 的直径,点 在 上,延长 至点 ,使 ,延长 与 的另一个交点为 ,连接 , .
(1)、求k的值;(2)、根据图象直接写出 的x的取值范围;(3)、 是线段AB上的一点,连接PC,PD,若 和 面积相等,求点P坐标.22. 如图, 为 的直径,点 在 上,延长 至点 ,使 ,延长 与 的另一个交点为 ,连接 , . (1)、求证: ;(2)、若 , ,求 的长.23. 如图,抛物线 经过 , 两点,顶点为D.
(1)、求证: ;(2)、若 , ,求 的长.23. 如图,抛物线 经过 , 两点,顶点为D.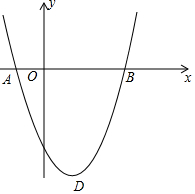 (1)、求a和b的值;(2)、将抛物线沿y轴方向上下平移,使顶点D落在x轴上.
(1)、求a和b的值;(2)、将抛物线沿y轴方向上下平移,使顶点D落在x轴上.求平移后所得图象的函数解析式;
若将平移后的抛物线,再沿x轴方向左右平移得到新抛物线,若 时,新抛物线对应的函数有最小值2,求平移的方向和单位长度.
24. 如图,已知四边形ABCD内接于⊙O,A是 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且 .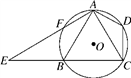 (1)、求证:△ADC∽△EBA;(2)、如果AB=8,CD=5,求tan∠CAD的值.25. 如图,在 中, ,以AC为直径的 与AB边交于点D,
(1)、求证:△ADC∽△EBA;(2)、如果AB=8,CD=5,求tan∠CAD的值.25. 如图,在 中, ,以AC为直径的 与AB边交于点D,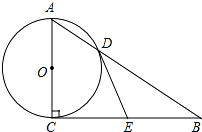 (1)、求证:DE是 的切线;(2)、若以点O、D、E、C为顶点的四边形是正方形,试判断 的形状,并说明理由.26. 如图 , 中, , , 为AB的中点, ,DE交AC于点G,DF经过点C.
(1)、求证:DE是 的切线;(2)、若以点O、D、E、C为顶点的四边形是正方形,试判断 的形状,并说明理由.26. 如图 , 中, , , 为AB的中点, ,DE交AC于点G,DF经过点C.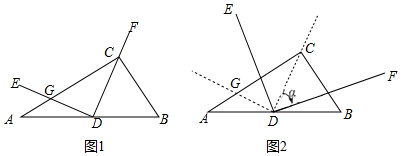 (1)、求 的值.(2)、如图②,将 绕点D顺时针方向旋转 , 的两边分别交AC于M,BC于 试判断 的值是否随着 的变化而变化?如果不变,请求出 的值;反之,请说明理由.27. 复习课中,教师给出关于x的函数 (k是实数).
(1)、求 的值.(2)、如图②,将 绕点D顺时针方向旋转 , 的两边分别交AC于M,BC于 试判断 的值是否随着 的变化而变化?如果不变,请求出 的值;反之,请说明理由.27. 复习课中,教师给出关于x的函数 (k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图象与坐标轴总有三个不同的交点;
③当 时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数;
教师:请你分别判断四条结论的真假,并给出理由,最后简单写出解决问题时所用的数学方法.
28. 如图 ,在四边形ABCD的边AB上任取一点 点P不与A,B重合 ,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.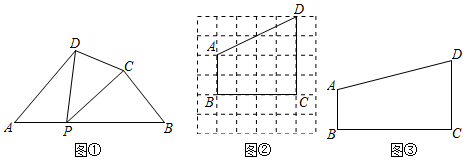
解决问题
(1)、如图①, ,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.(2)、如图②,在四边形ABCD中,A,B,C,D四点均在正方形网格 网格中每个小正方形的边长为 的格点 即每个小正方形的顶点 上,试在图 中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;(3)、如图③,在四边形ABCD中, , , , 点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.