江苏省南通市通州区2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 下列各点中,在函数y=﹣ 图象上的是( )A、(﹣3,﹣2) B、(﹣2,3) C、(3,2) D、(﹣3,3)2. 如果两个相似三角形的面积比是1:4,那么它们的周长比是A、1:16 B、1:6 C、1:4 D、1:23. 若抛物线y=ax2+bx+c与x轴的公共点的坐标是(﹣1,0),(5,0),则这条抛物线的对称轴是直线( )A、x=1 B、x=2 C、x=3 D、x=﹣24. 在一个不透明的布袋中,共有30个小球,除颜色外其他完全相同 若每次将球搅匀后摸一个球记下颜色再放回布袋 通过大量重复摸球试验后发现,摸到红色球的频率稳定在 左右,则口袋中红色球的个数应该是A、6个 B、15个 C、24个 D、12个5. 如图,将△ABC放在每个小正方形的边长都为1的网格中,点A,B,C均在格点上,则tanA的值是( )
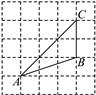 A、 B、 C、2 D、6. 若点 , , 在反比例函数 的图象上,则 , , 的大小关系是A、 B、 C、 D、7. 如图,PA,PB分别与 相切于A,B两点,PO与AB相交于点C, , ,则OC的长等于
A、 B、 C、2 D、6. 若点 , , 在反比例函数 的图象上,则 , , 的大小关系是A、 B、 C、 D、7. 如图,PA,PB分别与 相切于A,B两点,PO与AB相交于点C, , ,则OC的长等于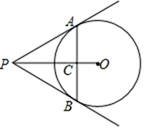 A、 B、3 C、 D、8. 若一个正多边形的一个内角是 ,则这个正多边形的中心角为A、 B、 C、 D、9. 若点 , 都在二次函数 的图象上,且 则m的取值范围是A、 B、 C、 D、10. 如图, 的半径为4,点A,B在 上,点P在 内, , ,如果 ,那么OP的长为
A、 B、3 C、 D、8. 若一个正多边形的一个内角是 ,则这个正多边形的中心角为A、 B、 C、 D、9. 若点 , 都在二次函数 的图象上,且 则m的取值范围是A、 B、 C、 D、10. 如图, 的半径为4,点A,B在 上,点P在 内, , ,如果 ,那么OP的长为 A、 B、3 C、 D、
A、 B、3 C、 D、二、填空题
-
11. 某一时刻身高160cm的小王在太阳光下的影长为80cm,此时他身旁的旗杆影长10m,则旗杆高为.12. 已知反比例函数 <,其图象在第二、四象限内,则k的取值范围是..13. 同时抛掷两枚硬币,恰好均为正面向上的概率是 .14. 在我国古代数学著作 九章算术 中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其大意为:如图,AB为 的直径,弦 于点E,若 寸, 寸,则 的直径等于寸
 15. 飞机着陆后滑行的距离s (单位:米)关于滑行的时间t (单位:秒)的函数表达式是 ,则飞机着陆后滑行的最长距离为米.16. 已知底面半径为4cm,母线长为12cm的圆锥,则它的侧面展开图的圆心角为17. 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E. 若AB=12,BM=5,则DE的长为.
15. 飞机着陆后滑行的距离s (单位:米)关于滑行的时间t (单位:秒)的函数表达式是 ,则飞机着陆后滑行的最长距离为米.16. 已知底面半径为4cm,母线长为12cm的圆锥,则它的侧面展开图的圆心角为17. 如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E. 若AB=12,BM=5,则DE的长为. 18. 在平面直角坐标系xOy中,若直线y=kx+5k(k为常数,k≠0)与抛物线y= x2相交于A,B两点,且OA⊥OB,则k的值为.19. 第一盒中有2个白球、1个红球,第二盒中有1个白球、1个红球,这些球除颜色外无其他差别,分别从每个盒中随机取出1个球.(1)、在第一盒中取出1个球是白球的概率是;(2)、求取出的2个球中1个白球、1个红球的概率.
18. 在平面直角坐标系xOy中,若直线y=kx+5k(k为常数,k≠0)与抛物线y= x2相交于A,B两点,且OA⊥OB,则k的值为.19. 第一盒中有2个白球、1个红球,第二盒中有1个白球、1个红球,这些球除颜色外无其他差别,分别从每个盒中随机取出1个球.(1)、在第一盒中取出1个球是白球的概率是;(2)、求取出的2个球中1个白球、1个红球的概率.三、解答题
-
20.(1)、计算: ;(2)、解方程: .21. 如图,在 中, , , 于 求证: .
 22. 如图,A(3,m)是反比例函数y= 在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y= 的图象于点P(2 , ).
22. 如图,A(3,m)是反比例函数y= 在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y= 的图象于点P(2 , ). (1)、求m的值和点B的坐标;(2)、连接AP,求△OAP的面积.23. 已知抛物线 与y轴交于点 与x轴的一个交点坐标是 .
(1)、求m的值和点B的坐标;(2)、连接AP,求△OAP的面积.23. 已知抛物线 与y轴交于点 与x轴的一个交点坐标是 . (1)、求此抛物线的顶点D的坐标;(2)、将此图象沿x轴向左平移2个单位长度,直接写出当 时x的取值范围.24. 如图,在△ABC中,∠C=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,与边BC交于点F,过点E作EH⊥AB于点H,连接BE
(1)、求此抛物线的顶点D的坐标;(2)、将此图象沿x轴向左平移2个单位长度,直接写出当 时x的取值范围.24. 如图,在△ABC中,∠C=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,与边BC交于点F,过点E作EH⊥AB于点H,连接BE (1)、求证:EH=EC;(2)、若AB=4,sinA= ,求AD的长.25. 某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.(1)、求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;(2)、该产品第一年的利润为24万元,那么该产品第一年的售价是多少?(3)、第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.26. 定义:如图 ,若点D在 的边AB上,且满足 ,则称满足这样条件的点为 的“理想点”
(1)、求证:EH=EC;(2)、若AB=4,sinA= ,求AD的长.25. 某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.(1)、求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;(2)、该产品第一年的利润为24万元,那么该产品第一年的售价是多少?(3)、第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.26. 定义:如图 ,若点D在 的边AB上,且满足 ,则称满足这样条件的点为 的“理想点” (1)、如图 ,若点D是 的边AB的中点, , ,试判断点D是不是 的“理想点”,并说明理由;(2)、如图 ,在 中, , , ,若点D是 的“理想点”,求CD的长;(3)、如图,已知平面直角坐标系中,点 , ,C为x轴正半轴上一点,且满足 ,在y轴上是否存在一点D,使点A,B,C,D中的某一点是其余三点围成的三角形的“理想点” 若存在,请求出点D的坐标;若不存在,请说明理由.27. 已知抛物线 与 形状相同,开口方向不同,其中抛物线 : 交x轴于A,B两点 点A在点B的左侧 ,且 ,抛物线 与 交于点A与 .
(1)、如图 ,若点D是 的边AB的中点, , ,试判断点D是不是 的“理想点”,并说明理由;(2)、如图 ,在 中, , , ,若点D是 的“理想点”,求CD的长;(3)、如图,已知平面直角坐标系中,点 , ,C为x轴正半轴上一点,且满足 ,在y轴上是否存在一点D,使点A,B,C,D中的某一点是其余三点围成的三角形的“理想点” 若存在,请求出点D的坐标;若不存在,请说明理由.27. 已知抛物线 与 形状相同,开口方向不同,其中抛物线 : 交x轴于A,B两点 点A在点B的左侧 ,且 ,抛物线 与 交于点A与 . (1)、求抛物线 , 的函数表达式;(2)、当x的取值范围是时,抛物线 与 上的点的纵坐标同时随横坐标的增大而增大;(3)、直线 轴,分别交x轴, , 于点 ,P,Q,当 时,求线段PQ的最大值.
(1)、求抛物线 , 的函数表达式;(2)、当x的取值范围是时,抛物线 与 上的点的纵坐标同时随横坐标的增大而增大;(3)、直线 轴,分别交x轴, , 于点 ,P,Q,当 时,求线段PQ的最大值.