江苏省南通市海门市2019届九年级上学期数学期末考试试卷
试卷更新日期：2020-01-08 类型：期末考试
一、单选题
-
1. ﹣3的相反数是（ ）A、 B、 C、 D、2. 下列计算中，正确的是（ ）A、a2•a4＝a8 B、（a2）4＝a6 C、a2+a4＝a6 D、a6÷a4＝a23. 若式子 在实数范围内有意义，则x的取值范围是（ ）A、x≤﹣3 B、x≥﹣3 C、x＜﹣3 D、x＞﹣34. 如图是某个几何体的三视图，该几何体是（ ）
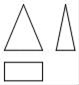A、圆锥 B、四棱锥 C、圆柱 D、四棱柱5. 下列说法正确的是（ ）A、要了解我市居民的低碳生活状况，适宜采用抽样调查的方法 B、一组数据2，2，3，6的众数和中位数都是2 C、“掷一枚硬币正面朝上的概率是 ”，表示每抛硬币2次就有1次正面朝上 D、随机抽取甲乙两名同学的5次数学成绩，平均分都是90分，方差分别是S甲2＝5，S乙2＝10，说明乙的成绩较为稳定6. 抛物线y＝﹣ （x﹣2）2+3的顶点坐标是（ ）A、（2，﹣3） B、（﹣2，3） C、（2，3） D、（﹣2，﹣3）7. 若关于x的不等式组 的解集为x＜3，则k的取值范围为（ ）A、k＞1 B、k＜1 C、k≥1 D、k≤18.如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为（ ）
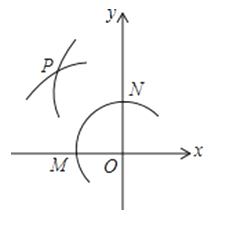A、a=b B、2a+b=﹣1 C、2a﹣b=1 D、2a+b=19. 端午节前夕举行了南通濠河国际龙舟邀请赛，在500米直道竞速赛道上，甲、乙两队所划行的路程y（单位：米）与时间t（单位：分）之间的函数关系式如图所示，根据图中提供的信息，有下列说法：①甲队比乙队提前0.5分到达终点②当划行1分钟时，甲队比乙队落后50米③当划行 分钟时，甲队追上乙队④当甲队追上乙队时，两队划行的路程都是300米其中错误的是（ ）
A、① B、② C、③ D、④10. 如图，在△ABC中，CA＝CB，∠C＝90°，点D是BC的中点，将△ABC沿着直线EF折叠，使点A与点D重合，折痕交AB于点E，交AC于点F，那么sin∠BED的值为（ ）
A、 B、 C、 D、二、填空题
-
11. 将数44000000用科学记数法表示为.12. 分解因式：x3﹣4x= ．13. 关于x的方程x2+mx+n＝0的两根为﹣2和3，则m+n的值为.14. 已知圆锥的底面半径为2cm，侧面积为10πcm2 ， 则该圆锥的母线长为cm.15. 如图，正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′，旋转角为α（0°≤α≤90°），若DE⊥B′C′，则∠α＝°
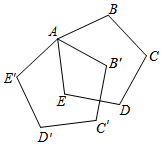16. 如果a﹣b＝5，ab＝2，则代数式|a2﹣b2|的值为.17. 如图（图1），在△ABC中，∠B＝45°，点P从△ABC的顶点出发，沿A→B→C匀速运动到点C，（图2）是点P运动时，线段AP的长度y随时间x变化的关系图象，其中M，N为曲线部分的两个端点，则△ABC的周长是.
18. 已知x＝﹣m和x＝m﹣2时，多项式ax2+bx+4a+1的值都相等，且m≠1，若当1＜x＜2时，存在x的值，使多项式ax2+bx+4a+1的值为3，则a的取值范围是.三、解答题
-
19.(1)、计算： ；(2)、先化简，再求代数式的值： ，其中 .20. 某专卖店有A，B两种商品.已知在打折前，买20件A商品和10件B商品用了400元；买30件A商品和20件B商品用了640元.A，B两种商品打相同折以后，某人买100件A商品和200件B商品一共比不打折少花640元，计算打了多少折？21. 某校开展了为期一周的“敬老爱亲”社会活动，为了解情况，学生会随机调查了部分学生在这次活动中做家务的时间，并将统计的时间（单位：小时）分成5组，A：0.5≤x＜1，B：1≤x＜1.5，C：1.5≤x＜2，D：2≤x＜2.5，E：2.5≤x＜3，制作成两幅不完整的统计图（如图）.
请根据图中提供的信息，解答下列问题：
(1)、学生会随机调查了名学生；(2)、补全频数分布直方图；(3)、若全校有900名学生，估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人？22. 甲、乙两名同学从《中国好声音》、《歌手》、《蒙面唱将猜猜猜》三个综艺节目中都随机选择一个节目观看.(1)、甲同学观看《蒙面唱将猜猜猜》的概率是；(2)、求甲、乙两名同学观看同一节目的概率.23. 如图，小明要测量河内小岛B到河边公路AD的距离，在点A处测得∠BAD＝37°，沿AD方向前进150米到达点C，测得∠BCD＝45°.求小岛B到河边公路AD的距离.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
24. 矩形AOBC中，OB＝4，OA＝3，分别以OB，OA所在直线为x轴，y轴，建立如图所示的平面直角坐标系，F是BC边上一个动点（不与B，C重合），过点F的反比例函数 （k＞0）的图象与边AC交于点E.
(1)、当点F为边BC的中点时，求点E的坐标；(2)、连接EF，求∠EFC的正切值.25. 如图，点D为圆O上一点，点C在直径AB的延长线上，且∠CAD＝∠BDC，过点A作⊙O的切线，交CD的延长线于点E.
(1)、求证：CD是⊙O的切线；(2)、若CB＝3，CD＝9，求ED的长.26. 已知二次函数y＝2x2+bx﹣1（b为常数）.(1)、若抛物线经过点（1，2b），求b的值；(2)、求证：无论b取何值，二次函数y＝2x2+bx﹣1图象与x轴必有两个交点；(3)、若平行于x轴的直线与该二次函数的图象交于点A，B，且点A，B的横坐标之和大于1，求b的取值范围.27. 已知，如图，矩形ABCD中，AD＝2，AB＝3，点E，F分别在边AB，BC上，且BF＝FC，连接DE，EF，并以DE，EF为边作▱DEFG.
(1)、求▱DEFG对角线DF的长；(2)、求▱DEFG周长的最小值；(3)、当▱DEFG为矩形时，连接BG，交EF，CD于点P，Q，求BP：QG的值.28. 如图，过原点O的直线与双曲线 交于上A（m，n）、B，过点A的直线交x轴正半轴于点D，交y轴负半轴于点E，交双曲线 于点P.
(1)、当m＝2时，求n的值；(2)、当OD：OE＝1：2，且m＝3时，求点P的坐标；(3)、若AD＝DE，连接BE，BP，求△PBE的面积.