江苏省淮安市淮阴区2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标是A、 B、 C、 D、2. 二次函数 有A、最大值 B、最小值 C、最大值 D、最小值3. 将抛物线 向左平移2个单位后,得到的抛物线的解析式是( ).A、 B、 C、 D、4. 在△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )A、 B、 C、 D、5. 如图,C岛在A岛的北偏东 方向,在B岛的北偏西 方向,则从C岛看A、B两岛的视角 的度数是
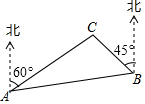 A、 B、 C、 D、6. 若相似△ABC与△DEF的相似比为1:3,则△ABC与△DEF的面积比为( )A、1:3 B、1:9 C、3:1 D、1:7. 如图,点D、E分别在AB、AC上,且 若 , , ;则AB的长为(
A、 B、 C、 D、6. 若相似△ABC与△DEF的相似比为1:3,则△ABC与△DEF的面积比为( )A、1:3 B、1:9 C、3:1 D、1:7. 如图,点D、E分别在AB、AC上,且 若 , , ;则AB的长为( A、16 B、8 C、10 D、58. 如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ,则四边形MABN的面积是( )
A、16 B、8 C、10 D、58. 如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC= ,则四边形MABN的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知 ,则 .10. 在 中, , , ,则 .11. 点 在二次函数 的图象上,则m的值是.12. 若二次函数 的图象与x轴没有交点,则m的取值范围是.13. 如图,在 的正方形网格中, .
 14. 为了测量某建筑物BE的高度(如图),小明在离建筑物15米(即DE=15米)的A处,用测角仪测得建筑物顶部B的仰角为45°,已知测角仪高AD=1.8米,则BE=米.
14. 为了测量某建筑物BE的高度(如图),小明在离建筑物15米(即DE=15米)的A处,用测角仪测得建筑物顶部B的仰角为45°,已知测角仪高AD=1.8米,则BE=米.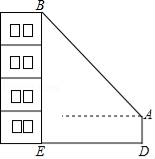 15. 如图,∠DAB=∠CAE,请补充一个条件: , 使△ABC∽△ADE.
15. 如图,∠DAB=∠CAE,请补充一个条件: , 使△ABC∽△ADE.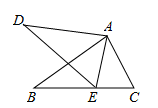 16. 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B'重合.若AB=2,BC=3,则△FCB'与△B'DG的面积比为.
16. 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B'重合.若AB=2,BC=3,则△FCB'与△B'DG的面积比为. 17. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为尺.
17. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为尺.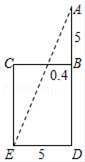
三、解答题
-
18. 求 的值.19. 如图,弦CD垂直于⊙O的直径AB,垂足为P,且CD=2 ,BP=1,求⊙O的半径.
 20. 已知:如图,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明.
20. 已知:如图,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明. 21. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)
21. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)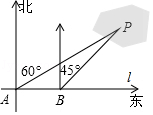 22. 如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
22. 如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点. (1)、试判断直线DE与⊙O的位置关系,并说明理由.
(1)、试判断直线DE与⊙O的位置关系,并说明理由.
(2)、若⊙O半径为2,∠B=60°,求图中阴影部分的面积.23. 如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接DE,AC (1)、求证:四边形ACDE为平行四边形;(2)、连接CE交AD于点O,若AC=AB=3,cosB= ,求线段CE的长.24. 课本中有一道作业题:
(1)、求证:四边形ACDE为平行四边形;(2)、连接CE交AD于点O,若AC=AB=3,cosB= ,求线段CE的长.24. 课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.

 (1)、如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.(2)、如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.25. 如图1是某段河床横断面的示意图 查阅该河段的水文资料,得到下表中的数据:
(1)、如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.(2)、如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.25. 如图1是某段河床横断面的示意图 查阅该河段的水文资料,得到下表中的数据:5
10
20
30
40
50
2
8
 (1)、请你以上表中的各对数据 作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;(2)、①填写下表:
(1)、请你以上表中的各对数据 作为点的坐标,尝试在图2所示的坐标系中画出y关于x的函数图象;(2)、①填写下表:x
5
10
20
30
40
50
②根据所填表中数据呈现的规律,猜想出用x表示y的二次函数的表达式:;
(3)、当水面宽度为36米时,一艘吃水深度 船底部到水面的距离 为 米的货船能否在这个河段安全通过?为什么?26. 如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点P从点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设点P的运动时间为x(秒). (1)、用含有x的代数式表示CE的长;(2)、求点F与点B重合时x的值;(3)、当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式;(4)、当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.
(1)、用含有x的代数式表示CE的长;(2)、求点F与点B重合时x的值;(3)、当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式;(4)、当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.