湖北省襄阳市襄州2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

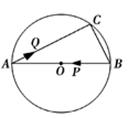
1. 将方程 $x^{2} + 2 x - 5 = 0$ 的左边配成完全平方式后所得的方程是（）

A、 ${(x + 2)}^{2} = 5$ B、 ${(x + 1)}^{2} = 6$ C、 ${(x + 1)}^{2} = 5$ D、 ${(x + 2)}^{2} = 6$

查看试题解析
2. 如图是一个中心对称图形，A为对称中心，若∠C=90°，∠B=60°，BC=1，则BB’的长为（）

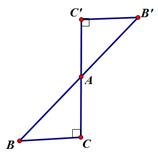A、4 B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
3. 若△ABC∽△DEF，△ABC与△DEF的相似比为2︰3，则S_△ABC︰S_△DEF为（）

A、2∶3 B、4∶9 C、 $\sqrt{2}$ ∶ $\sqrt{3}$ D、3∶2

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ $(k \neq 0)$ 的图象经过点 $P$ (﹣2，3)，则该函数的图象不经过的点是（）

A、(3，-2) B、(1，-6) C、(-1，6) D、(6，1)

查看试题解析
5. 用一枚质地均匀的硬币做抛掷试验，前10次掷的结果都是正面向上，如果下一次掷得的正面向上的概率为P(A)，则（）

A、P(A)＝1 B、P(A)＝ $\frac{1}{2}$ C、P(A)＞ $\frac{1}{2}$ D、P(A)＜ $\frac{1}{2}$

查看试题解析
6. 下列命题：①等弧所对的圆周角相等；②平分弦的直径垂直于弦；③等边三角形的外心也是它的内心；④正五边形既是轴对称图形，也是中心对称图形.其中正确的命题是（）

A、①③ B、②④ C、①②③ D、①②③④

查看试题解析
7. 某新建火车站站前广场绿化工程中有一块长为20米，宽为12米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为112米² ，两块绿地之间及周边留有宽度相等的人行通道(如图所示)，问人行通道的宽度是（）

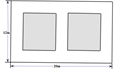A、2米 B、 $\frac{32}{3}$ 米 C、2米或 $\frac{32}{3}$ 米 D、3米

查看试题解析
8. 如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB＝1.2米，BP＝1.8米，PD＝12米，那么该古城墙的高度是（）

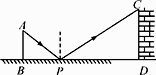A、6米 B、8米 C、18米 D、24米

查看试题解析
9. 如图，在平面直角坐标中，过格点A，B，C做一圆弧，点B与下列格点的连线中，能够与该圆弧相切的格点的坐标是（）

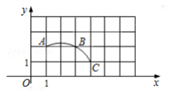A、(0，3) B、(5，1) C、(6，1) D、(7，1)

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ $(a < 0)$ 的图象如图所示，则下列结论：
① $a c < 0$ ；②方程 $a x^{2} + b x + c = 0$ 有两个不相等的异号根； $③ y$ 随 $x$ 的增大而增大；④ $a - b + c < 0$ ，其中正确的个数（）

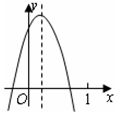A、4个 B、3个 C、2个 D、1个

查看试题解析

二、解答题

11. 解方程

(1)、 $(x - 2) (x + 4) = 6$

(2)、 ${(x + 1)}^{2} - 9 {(x + 3)}^{2} = 0$

查看试题解析
12. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2} ， \frac{1}{4} ， 1$ 的卡片，乙同学手中藏有三张分别标有数字1，3，2的卡片，卡片外形相同.现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为 $a ， b$ .

(1)、请你用树形图或列表法列出所有可能的结果.

(2)、现制定这样一个游戏规则：若所选出的 $a ， b$ 能使得 $a x^{2} + b x + 1 = 0$ 有两个不相等的实数根，则甲获胜；否则乙获胜.请问这样的游戏规则公平吗？请你用概率知识解释

查看试题解析
13. 把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AGFE，边FG与BC交于点H.

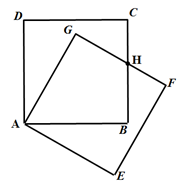(1)、试问线段HG与线段HB相等吗？请先观察猜想，然后再证明你的猜想；

(2)、若正方形的边长为2cm，∠BAG＝2∠BAE，求重叠部分(四边形ABHG)的面积.

查看试题解析
14. 如图，已知△ABC内接于⊙O，点D在OC的延长线上，∠ABC＝∠CAD.

(1)、若∠ABC＝20º，则∠OCA的度数为；

(2)、判断直线AD与⊙O的位置关系，并说明理由.

查看试题解析
15. 如图，已知直线 $y = \frac{1}{2} x$ 与双曲线 $y = \frac{k}{x}$ $(k > 0)$ 交于A，B两点，且点A的横坐标为4。

(1)、求 $k$ 的值；

(2)、直接写出当 $\frac{k}{x} > \frac{1}{2} x$ 时 $x$ 的取值范围；

(3)、若双曲线 $y = \frac{k}{x}$ $(k > 0)$ 上一点C的纵坐标为8，求△AOC的面积；

查看试题解析
16. 某公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和成本进行了调研，结果如下：一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲)，一件商品的成本Q(元)与时间t(月)的关系可用一段抛物线上的点来表示，其中6月份成本最高(如图乙).根据图象提供的信息解答下面的问题：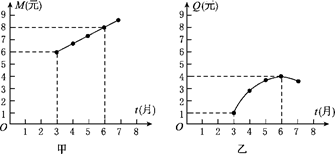

(1)、一件商品在3月份出售时的利润是多少元？(利润＝售价－成本)

(2)、求出一件商品的成本Q(元)与时间t(月)之间的函数关系式；

(3)、你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗？若该公司能在一个月内售出此种商品30 000件，请你计算该公司在一个月内最少获利多少元？

查看试题解析
17. 如图，△ABC和△DEF都是等腰直角三角形，∠ACB＝∠EFD＝90º，△DEF，的顶点E与△ABC的斜边AB的中点重合.将△DEF绕点E旋转，旋转过程中，线段AC与线段EF相交于点Q，射线ED与射线BC相交于点P.

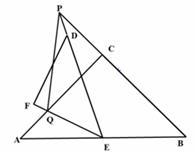(1)、求证：△AEQ∽△BPE；

(2)、求证：PE平分∠BPQ；

(3)、当AQ＝2，AE= $3 \sqrt{2}$ ，求PQ的长.

查看试题解析
18. 已知如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴相交于B(1，0)，C(5，0)两点，与y轴的正半轴相交于A点，过A，B，C三点的⊙P与y轴相切于点A，M为 $y$ 轴负半轴上的一个动点，直线MB交抛物线于N，交⊙P于D.

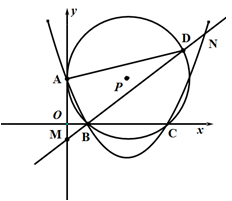(1)、填空：A点坐标是， ⊙P半径的长是， $a$ = ， $b$ = ， $c$ =；

(2)、若S_△_BNC：S_△_AOB＝48：5，求N点的坐标；

(3)、若△AOB与以A，B，D为顶点的三角形相似，求MB·MD的值.

查看试题解析

三、填空题

19. 方程（x+3）（x+2）＝x+3的解是.

查看试题解析
20. 已知方程 $x^{2} - 7 x + 12 = 0$ 的两根恰好是Rt△ABC的两条直角边长，则Rt△ABC内切圆的半径为.

查看试题解析
21. 将抛物线 $y = \frac{2}{3} x^{2} - 1$ 向右平移3个单位，再向上平移3个单位，所得的抛物线的解析式为.

查看试题解析
22. 如图，点F是等边△ABC内一点，将△ABF绕点B按顺时针方向旋转60°得△CBG，连接FG，则△BFG的形状是.

查看试题解析
23. 如图，AB是⊙O的直径，弦BC=6cm，AC=8cm．若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q以1cm/s的速度从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t(s)，当△APQ是直角三角形时，t的值为．

查看试题解析