辽宁省大连市西岗区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 下列四个交通标志图中,是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、a2+a3=a5 B、a6÷a2=a3 C、(a2)3=a6 D、2a×3a=6a3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
2. 下列计算正确的是( )A、a2+a3=a5 B、a6÷a2=a3 C、(a2)3=a6 D、2a×3a=6a3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )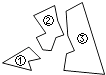 A、带①去 B、带②去 C、带③去 D、带①和②去4. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( )A、5.6×10﹣1 B、5.6×10﹣2 C、5.6×10﹣3 D、0.56×10﹣15. 如图,AC与BD交于O点,若 ,用“SAS”证明 ≌ ,还需
A、带①去 B、带②去 C、带③去 D、带①和②去4. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( )A、5.6×10﹣1 B、5.6×10﹣2 C、5.6×10﹣3 D、0.56×10﹣15. 如图,AC与BD交于O点,若 ,用“SAS”证明 ≌ ,还需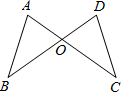 A、 B、 C、 D、6. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、7. 若把分式 中的x和y同时扩大为原来的10倍,则分式的值A、扩大10倍 B、缩小10倍 C、缩小100倍 D、保持不变8. 若等腰三角形底角为72°,则顶角为A、108° B、72° C、54° D、36°9. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、10. 如图(图在第二页)所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A、 B、 C、 D、6. 下列各式由左边到右边的变形中,是分解因式的为( )A、 B、 C、 D、7. 若把分式 中的x和y同时扩大为原来的10倍,则分式的值A、扩大10倍 B、缩小10倍 C、缩小100倍 D、保持不变8. 若等腰三角形底角为72°,则顶角为A、108° B、72° C、54° D、36°9. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、10. 如图(图在第二页)所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( ) A、13 B、26 C、47 D、94
A、13 B、26 C、47 D、94二、填空题
-
11. 若等腰三角形的边长分别为3和6,则它的周长为.12. 当 时,分式 有意义.13. 因式分解:x2-9= .
14. 如图,在 中, ,CD是 的平分线,若 ,则D到AC的距离为. 15. 如果实数a,b满足a+b=6,ab=8,那么a2+b2=.16. 直角三角形纸片的两直角边长分别为6,8,现将 如图那样折叠,使点A与点B重合,折痕为DE,则AE的长为.
15. 如果实数a,b满足a+b=6,ab=8,那么a2+b2=.16. 直角三角形纸片的两直角边长分别为6,8,现将 如图那样折叠,使点A与点B重合,折痕为DE,则AE的长为.
三、解答题
-
17. 计算:(1)、(2)、先化简,再求值:(2x+3y)2﹣(2x+y)(2x﹣y),其中x= ,y=﹣1.18. 计算(1)、 ;(2)、 .19. 解方程:20. 如图,点A、B、C、D在同一条直线上, , , .
求证: .
 21. 如图,在长方形ABCD中,把 沿对角线BD折叠得到 ,线段BE与AD相交于点P,若 , .
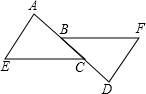
21. 如图,在长方形ABCD中,把 沿对角线BD折叠得到 ,线段BE与AD相交于点P,若 , .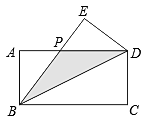 (1)、求BD长度 用含m的式子表示 ;(2)、若点P到BD的距离为 ,试求此时m的值.22. 如图,在等腰 中, ,D为底边BC延长线上任意一点,过点D作 ,与AC延长线交于点E.
(1)、求BD长度 用含m的式子表示 ;(2)、若点P到BD的距离为 ,试求此时m的值.22. 如图,在等腰 中, ,D为底边BC延长线上任意一点,过点D作 ,与AC延长线交于点E. (1)、则 的形状是;(2)、若在AC上截取 ,连接FB、FD,判断FB、FD的数量关系,并给出证明.23. 如图,P为正方形ABCD的边BC上一动点(P与B. C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)、则 的形状是;(2)、若在AC上截取 ,连接FB、FD,判断FB、FD的数量关系,并给出证明.23. 如图,P为正方形ABCD的边BC上一动点(P与B. C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M. (1)、求证:AP⊥BQ;(2)、若AB=3,BP=2PC,求QM的长;(3)、当BP=m,PC=n时,求AM的长。24. 阅读下列材料:
(1)、求证:AP⊥BQ;(2)、若AB=3,BP=2PC,求QM的长;(3)、当BP=m,PC=n时,求AM的长。24. 阅读下列材料:小明遇到这样问题:
如图1,在 中, ,在AB上取一点D,在AC延长线上取一点E,若 ,判断PD与PE的数量关系.

小明通过思考发现,可以采用两种方法解决向题:
方法一:过点D作 ,交BC于F,即可解决向题;
方法二:过点D、点E分别向直线BC引垂钱,垂足分别是F、G,也可解决问题.
(1)、请回答:PD与PE的数量关系是;(2)、任选上述两种方法中的一种方法,在图1中补全图象,并给出证明;(3)、如图2,在 中, ,将AC绕点A顺时针旋转 度后得到AD,过点D作 ,交AB于点E, ,则图中是否存在与DE相等的线段,请找出来并给出证明.25. 如图,在平面直角坐标系中,点 , , , ,且 , ,连接DE,点F是DE的中点,连接AF. (1)、 ;(2)、猜想AF的长并说明理由;(3)、直接写出 的面积是.
(1)、 ;(2)、猜想AF的长并说明理由;(3)、直接写出 的面积是.