辽宁省大连市普兰店区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 线段AB的垂直平分线上一点P到A点的距离PA=5,则点P到B点的距离PB等于（）

A、PB=5 B、PB>5 C、PB<5 D、无法确定

查看试题解析
2. 四边形内角和是（）

A、180° B、360° C、480° D、540°

查看试题解析
3. 已知△ABC的三条边长都是整数,其中两条边长分别为 $a = 1 、 b = 2 ，$ 则第三条边长 $c$ 等于（）

A、1 B、2 C、3 D、1或2

查看试题解析
4. 下列各个式子运算的结果是 $8 a^{5}$ 的是（）

A、 $2 a^{2} + 6 a^{3}$ B、 ${(2 a^{2})}^{3}$ C、 $8 a^{7} - 8 a^{2}$ D、2a² $\cdot$ 4a³

查看试题解析
5. 下列因式分解，其中正确的是（）

A、 $x^{2} - 6 x - 9 = {(x - 3)}^{2}$ B、 $x^{2} - a^{2} = {(x - a)}^{2}$ C、 $2 x^{2} - 6 x = 2 x (x - 6)$ D、 $x^{2} - 3 x + 2 = (x - 2) (x - 1)$

查看试题解析
6. 把分式 $- \frac{8 a^{6} b}{12 a^{2} b^{2}}$ 约分结果是（）

A、 $- \frac{a^{4}}{4 b}$ B、 $- \frac{a^{3}}{4 b}$ C、 $- \frac{2 a^{4}}{3 b}$ D、 $- \frac{2 a^{3}}{3 b}$

查看试题解析
7. 如图，在△ABC与△BAD中，AC=BD，若使△ABC≌△BAD，还需要增加下列一个条件（）

A、∠C=∠D B、∠BAC=∠ABD C、AE=BE D、CE=DE

查看试题解析
8. 如图，正五边形ABCDE中，直线 $l$ 过点B，且 $l$ ⊥ED，下列说法：① $l$ 是线段AC的垂直平分线；②∠BAC=36°；③正五边形ABCDE有五条对称轴.正确的有（）.

A、①② B、①③ C、②③ D、①②③

查看试题解析
9. 如果分式 $\frac{x^{2} - 4}{x^{2} - 4 x + 4}$ 的值为0，则 $x$ 的值为（）

A、 $- 2$ B、 $2$ C、 $\pm 2$ D、不存在

查看试题解析
10. 如图，在直角坐标系中，点A的坐标为(3，-2)，直线MN∥ $x$ 轴且交 $y$ 轴于点C(0，1），则点A关于直线MN的对称点的坐标为（）

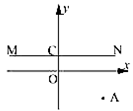A、(-2，3) B、(-3，-2) C、(3，4) D、(3，2)

查看试题解析

二、填空题

11. 如图，在△ABC中，∠BAC=35°，延长AB到点D，∠CBD=65°，过顶点A作AE∥BC，则∠CAE=°.

查看试题解析
12. 如图，在△ABC中，∠ACB=90°，∠B=30°，CD⊥AB，垂足是D，若AB=8cm，则AD=cm.

查看试题解析
13. 已知 $x^{2} - y^{2} = 2019$ ， $y = x - 3$ 则 $x + y =$ 。

查看试题解析
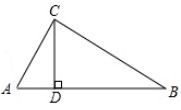14. 如图，△ABC≌△DEC，其中AB与DE是对应边，AC与DC是对应边，若∠A=∠30°，∠CEB=70°，则∠ACD=°.

查看试题解析
15. 假期，某校为了勤工俭学,要完成整个A小区的绿化工作，开始由七年级单独工作了4天，完成整个绿化工作的三分之一，这时九年级也参加工作，两个年级又共同工作了2天，才全部完成整个绿化工作，则由九年级单独完成整个绿化工作需要天.

查看试题解析
16. 关于 $x$ 的方程 $\frac{x + 2 t}{2 x - 3} = 1$ 的解是正数,则 $t$ 的取值范围是.

查看试题解析

三、解答题

17. 解方程： $\frac{1 - x}{x - 2} = 1 - \frac{3}{x - 2}$ .

查看试题解析
18. 先化简，再求值： $(\frac{2 x}{2 x + 1} - \frac{1}{4 x^{2} + 2 x}) \div (1 - \frac{4 x^{2} + 1}{4 x}) ，$ 其中 $x = 3.$

查看试题解析
19. 如图，将一张长方形的纸条ABCD沿EF折叠，AD交 $EC'$ 于点G，若折叠后 $∠ AGC' = 48 ° ，$

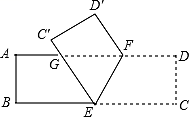(1)、求∠CEF的度数；

(2)、求证：△EFG是等腰三角形.

查看试题解析
20. 如图，点A、D、C、F在同一直线上，AB∥EE，AB=EF，AD=CF.
求证：△ABC≌△FED

查看试题解析
21. 如图，点E在长方形ABCD的边BC上，AE⊥EF，点F在边CD上，已知EC=AB=3cm，BC=5cm.
求四边形AEFD的面积.

查看试题解析
22.

(1)、计算: $2018^{2} - 2019 \times 2017$ ；

(2)、已知 $2 x - 5 y - 5 = 0 ，$ 且 $x 、 y$ 均为整数,求 $4^{x} \cdot 32^{- y}$ 的值.

查看试题解析
23. 已知: $a + b = 5 ， ab = 4.$

(1)、求 $a^{2} + b^{2}$ 的值；

(2)、若 $a > b ，$ 求 $a - b$ 的值；

(3)、若 $a > b ，$ 分别求出 $a$ 和 $b$ 的值.

查看试题解析
24. 一辆轿车和一辆货车同时从甲地出发，已知轿车的速度比货车的速度每小时快20千米，当轿车行驶到距甲地360千米的丙地时，货年恰好行驶到距离甲地300千米的乙地，问轿车与货车的速度分别是多少？

查看试题解析
25. 如图，已知△ABC是等边三角形，D是AB边上任意一点，∠CDE=60°，DE与∠ABC外角平分线相交于点E.

(1)、求证：CD=DE；

(2)、若D是AB延长线上任意一点，∠CDE=60°，DE与∠ABC外角平分线相交于点E.请画出图形，判断CD=DE是否还成立?若成立，请给予证明；若不成立，请说明理由.

查看试题解析