辽宁省大连市金普新区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是轴对称图形的是（）

A、 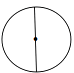B、 C、 D、

查看试题解析
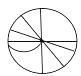2. 肥皂泡的泡壁厚度大约是 $0 .00000071$ 米，数字 $0 .00000071$ 用科学记数法表示为（）

A、 $7 .1 \times 10^{7}$ B、 $71 \times 10^{-8}$ C、 $0 .71 \times 10^{-6}$ D、 $7 .1 \times 10^{-7}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{3} • a^{2} = a^{6}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $a^{6} \div a^{3} = a^{^{2}}$

查看试题解析
4.
如图，△ACB≌△A′CB′，∠ACA′=30°，则∠BCB′的度数为（　　）

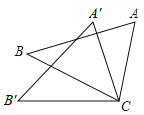A、20° B、30° C、35° D、40°

查看试题解析
5. 经过以下变化后得到的三角形不能和 $△ A B C$ 全等的是（）

A、平移 B、翻折 C、旋转 D、放大

查看试题解析
6. 等腰三角形的顶角为 $80^{\circ}$ ，则底角的度数是（）

A、 $40^{\circ}$ B、 $50^{\circ}$ C、 $80^{^{\circ}}$ D、 $100^{^{\circ}}$

查看试题解析
7. 分式 $\frac{x^{2} - 4}{x + 2}$ 的值为零，则 $x$ 的值为（）

A、 $2$ B、 $0$ C、 $- 2$ D、 $\pm 2$

查看试题解析
8. 如图：已知∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD=（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

9. 使式子 $\sqrt{\frac{1}{2 x + 3}}$ 有意义的实数 $x$ 的取值是.

查看试题解析
10. 若点 $P$ 的坐标是 $(- 6 ， 8)$ ，则点 $P$ 关于 $y$ 轴对称的点的坐标是 .

查看试题解析
11. 若 $(x + a) (x + b) = x^{2} + 6 x + 5 ，$ 则 $a + b$ 的值为 .

查看试题解析
12. 分解因式： $3 a x^{2} - 12 a y^{2} =$ .

查看试题解析
13. 若 $x^{2} - m x + 81$ 是一个完全平方式，则 $m$ 的值为.

查看试题解析
14. 化简： $\frac{3}{\sqrt{6}} =$ .

查看试题解析
15. 计算： $(12 a^{3} + 6 a^{2} - 3 a) \div 3 a =$

查看试题解析
16. 如图，在 $2 \times 2$ 的正方形格纸中，有一个以格点为顶点的 $△ A B C$ ，在格纸中能画出与 $△ A B C$ 成轴对称且也以格点为顶点的三角形（不包括 $△ A B C$ 本身），这样的三角形共有个.

查看试题解析

三、解答题

17. 计算： $(\sqrt{5} - 2) (\sqrt{5} + 2) - \sqrt{12} + {(- 3)}^{^{0}} - {(\frac{1}{2})}^{- 1}$ .

查看试题解析
18. 如图， $C$ 是 $A B$ 的中点， $A D / / C E ， A D = C E$ ，求证：.

查看试题解析
19. 计算 $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) \div \frac{x - 4}{x}$

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90^{\circ} ， D$ 是 $B C$ 上一点（ $D$ 与 $C$ 不重合）.

(1)、尺规作图：过点 $D$ 作 $B C$ 的垂线 $D E$ 交 $A B$ 于点 $E$ ，作 $∠ B A C$ 的平分线 $A F$ 交 $D E$ 于点 $F$ ，交 $B C$ 于点 $H$ （保留作图痕迹，不用写作法）；

(2)、求证： $E F = A E .$

查看试题解析
21. 列方程解应用题
甲、乙两名学生练习打字，甲打 $135$ 个字所用时间于乙打 $180$ 个字所用时间相同，已知甲平均每分钟比乙少打 $15$ 个字，求甲平均每分钟打字的个数.

查看试题解析
22. 一商店在某时间以每件 $m$ 元的价格卖出两件衣服，其中一件盈利 $n %$ ，另一件亏损 $n %$ ，卖这两件衣服总的是盈利还是亏损，或是不赢不亏？说明理由.

查看试题解析
23. 在 $△ A B C$ 中， $∠ A C B = 45^{\circ} ， A D ⊥ B C$ 垂足为 $D$ ，点 $E$ 在 $A D$ 上， $E D = B D ，$ 连接 $C E$ 并延长交 $A B$ 于点 $F$ ，连接 $D F$ .

(1)、求证： $∠ B A D = ∠ E C D ；$

(2)、求证： $∠ D F E = 45^{\circ} .$

查看试题解析
24. 如图，在等边 $△ A B C$ 中，点 $D ， E$ 分别在边 $A B ， B C$ 上， $A D = B E$ ，线段 $A E ， C D$ 交于点 $F .$

(1)、求证： $A E = C D ；$

(2)、连接 $B F$ ，当 $∠ B F C = 90^{\circ}$ 时，求证： $C F = 2 A F$ .

查看试题解析
25. 如图1，长方形 $A B C D$ 中， $A B = 9 c m ， B C = 6 c m ，$ 点 $P$ 从点 $A$ 出发，沿 $A \to B \to C \to D$ 运动，同时，点 $Q$ 从点 $B$ 出发，沿 $M^{'}$ 运动，当点 $P$ 到达点 $B$ 时，点 $Q$ 恰好到达点 $C$ ，已知点 $P$ 每秒比点 $Q$ 每秒多运动 $1 c m ，$ 当其中一点到达 $D$ 时，另一点停止运动.

(1)、求 $P ， Q$ 两点的运动速度；

(2)、当其中一点到达点 $D$ 时，另一点距离 $D$ 点 $c m$ （直接写答案）；

(3)、设点 $P ， Q$ 的运动时间为 $t$ 秒 $(t > 0)$ ，请用含 $t$ 的代数式表示 $△ A P Q$ 的面积 $S$ ，并写出 $t$ 的取值范围.

查看试题解析
26. 数学课上张老师将课本 $44$ 页第 $4$ 题进行了改编，图形不变.请你完成下面问题.

(1)、如图， $∠ A C B = ∠ A D B ， B C = B D$ .求证： $△ A B C ≅ △ A B D .$

(2)、如图， $∠ C A B = ∠ D A B ， B C = B D$ .求证： $△ A B C ≅ △ A B D .$

(3)、如图， $∠ A B C = ∠ A B D ， A C = A D .$ 求证： $△ A B C ≅ △ A B D .$

查看试题解析