江苏省扬州市高邮市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案分别是清华、北大、人大、复旦大学的校徽，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列一组数： $\sqrt[3]{8}$ ， $\frac{22}{7}$ ，- $\frac{π}{3}$ ， $\sqrt{8}$ ，0.080080008…（相邻两个8之间依次增加一个0）其中无理数的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
3. 蓝鲸是世界上体积最大的动物，有一只蓝鲸的体重约为1.68×10⁵kg，1.68×10⁵这个近似数它精确到（）

A、百位 B、百分位 C、千分位 D、千位

查看试题解析
4. 在平面直角坐标系中，若将原图形上的每个点的横坐标都加上3，纵坐标保持不变，则所得图形的位置与原图形相比（）

A、向上平移3个单位 B、向下平移3个单位 C、向右平移3个单位 D、向左平移3个单位

查看试题解析
5. 若等腰三角形的底边长为6，底边上的中线长为4，则它的腰长为（）

A、7 B、6 C、5 D、4

查看试题解析
6. 一次函数y=3x﹣2的图象上有两点A（﹣1，y₁），B（﹣2，y₂），则y₁与y₂的大小关系为（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁=y₂ D、不能确定

查看试题解析
7. 在同一平面直角坐标系中，直线y=x-2与直线y=- $\frac{1}{2}$ x-b的交点一定不在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图，在△ABC中，AB=3cm、AC=4cm、BC=5cm，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画的条数为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

9. 分式 $\frac{1}{4 a^{2} b^{3}}$ 、 $\frac{1}{6 a^{3} b}$ 的最简公分母是.

查看试题解析
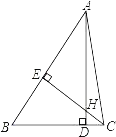
10. 在函数 $y = \frac{\sqrt{x - 4}}{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
11. 如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：，使△AEH≌△CEB.

查看试题解析
12. 若m为整数，且 $\sqrt{5}$ ＜m＜ $\sqrt{10}$ ，则m=.

查看试题解析
13. 若直角三角形的两直角边a，b满足 $\sqrt{a - 8}$ +b²-12b+36=0，则斜边c上中线的长为.

查看试题解析
14. 一个正数a的平方根分别是2m﹣1和﹣3m+ $\frac{5}{2}$ ，则这个正数a为．

查看试题解析
15. 已知点A（m-1，-5）和点B（2，m+1），若直线AB∥x轴，则线段AB的长为.

查看试题解析
16. 已知点O是△ABC的三条角平分线的交点，若△ABC的周长为12cm，面积为36cm² ，则点O到AB的距离为cm.

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，CE平分∠ACD交AB于E，若AC=2，AE=1，则BC=.

查看试题解析
18. 已知点A（2m-1，4m+2015）、B（- $\frac{1}{2}$ n+ $\frac{3}{2}$ ，-n+2020）在直线y=kx+b上，则k+b值为.

查看试题解析

三、解答题

19. 解分式方程：

(1)、 $\frac{x}{x + 2} = \frac{2}{x - 1} + 1$ ；

(2)、 $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$

查看试题解析
20. 先化简代数式 $(\frac{x}{x + 3} - \frac{x - 3}{x^{2} - 9}) \div \frac{x^{2} - 2 x + 1}{x + 3}$ ，再从0≤x≤3的范围内选择一个合适的整数代入求值.

查看试题解析
21. 甲、乙两人在笔直的道路AB上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，假设他们分别以不同的速度匀速行驶，甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人之间的距离y（千米）与甲出发的时间x（分）之间的函数图象如图.

(1)、A地与B地相距km，甲的速度为km/分；

(2)、求甲、乙两人相遇时，乙行驶的路程；

(3)、当乙到达终点A时，甲还需多少分钟到达终点B？

查看试题解析
22. （ $\frac{1}{2}$ ）^-1-|2- $\sqrt{3}$ |-（π-3.14）⁰+ $\sqrt{{(- 2)}^{2}}$

查看试题解析
23. 如图，在平面直角坐标系中，已知△ABC的顶点坐标分别为A（-3，5），B（-2，1），C（-1，3）.

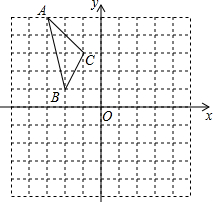(1)、①将△ABC向右平移3个单位得到△A₁B₁C₁ ，请画出平移后的△A₁B₁C₁；
②将△A₁B₁C₁沿x轴翻折得到△A₂B₂C₂ ，请画出翻折后的△A₂B₂C₂；

(2)、若点P（m，n）是△ABC内一点，点Q是△A₂B₂C₂内与点P对应的点，则点Q坐标.

查看试题解析
24. 如图，四边形ABCD中，对角线AC、BD交于点O，AB=AC，点E是BD上一点，且AE=AD，∠EAD=∠BAC.

(1)、求证：∠ABD=∠ACD；

(2)、若∠ACB=62°，求∠BDC的度数.

查看试题解析
25. 如图，直线y= $\frac{2}{3}$ x+4与x轴相交于点A，与y轴相交于点B.

(1)、求△AOB的面积；

(2)、过B点作直线BC与x轴相交于点C，若△ABC的面积是16，求点C的坐标.

查看试题解析
26. 2020年8月高邮高铁将通车，高邮至北京的路程约为900km，甲、乙两人从高邮出发，分别乘坐汽车A与高铁B前往北京.已知A车的平均速度比B车的平均速度慢150km/h，A车的行驶时间是B车的行驶时间的2.5倍，两车的行驶时间分别为多少？

查看试题解析
27. 在平面直角坐标系xOy中，有一点P（a，b），实数a，b，m满足以下两个等式：2a-6m+4=0，b+2m-8=0.

(1)、当a=1时，点P到x轴的距离为；

(2)、若点P在第一三象限的角平分线上，求点P的坐标；

(3)、当a＜b时，则m的取值范围是.

查看试题解析
28. 如图1，在平面直角坐标系中，△OAB是等边三角形，点B的坐标为（4，0），点C（a，0）是x轴上一动点，其中a≠0，将△AOC绕点A逆时针方向旋转60°得到△ABD，连接CD.

(1)、求证；△ACD是等边三角形；

(2)、如图2，当0＜a＜4时，△BCD周长是否存在最小值？若存在，求出a的值；若不存在，请说明理由.

(3)、如图3，当点C在x轴上运动时，是否存在以B、C、D为顶点的三角形是直角三角形？若存在，求出a的值；若不存在，请说明理由.

查看试题解析