江苏省南通市通州区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 下列计算中,正确的是( )A、 B、 C、 D、2. 若使分式 有意义,x的取值是( )A、 B、 C、 D、3. 人体中红细胞的直径约为0.0000077米,将0.0000077用科学记数法表示为( )A、7.7×10﹣6 B、7.7×10﹣5 C、0.77×10﹣6 D、0.77×10﹣54. 下列式子为最简二次根式的是( )A、 B、 C、 D、5. 如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
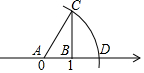 A、 B、 C、 D、6. 如图, 中, 于D, 于E,AD交BE于点F,若 ,则 等于
A、 B、 C、 D、6. 如图, 中, 于D, 于E,AD交BE于点F,若 ,则 等于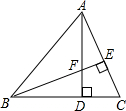 A、 B、 C、 D、7. 有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )A、 B、 C、 D、8. 如图,在△ABC中,BA=BC,BP,CQ是△ABC的两条中线,M是BP上的一个动点,则下列线段的长等于AM+QM最小值的是( )
A、 B、 C、 D、7. 有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克.设第一块试验田每亩收获蔬菜xkg,根据题意,可得方程( )A、 B、 C、 D、8. 如图,在△ABC中,BA=BC,BP,CQ是△ABC的两条中线,M是BP上的一个动点,则下列线段的长等于AM+QM最小值的是( )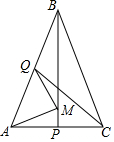 A、AC B、CQ C、BP D、BC9. 锐角△ABC中,AB=a-1,AC=a,BC=a+1(a>4),BD⊥AC于点D.则CD-DA的值为( )A、 B、2 C、 D、4
A、AC B、CQ C、BP D、BC9. 锐角△ABC中,AB=a-1,AC=a,BC=a+1(a>4),BD⊥AC于点D.则CD-DA的值为( )A、 B、2 C、 D、4二、填空题
-
10. 点A(1,-2)关于x轴对称的点的坐标是.11. 计算(a-1)(2a+1)=.12. 已知xm=6,xn=3,则xm-n的值为.13. 关于x的方程 的解为x=1,则a=.14. 如图,△ABC中,D是BC上一点,AC=AD=BD,若∠DAC=84°,则∠B=度.
 15. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,若AE= ,AD= ,则BC的长为.
15. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,若AE= ,AD= ,则BC的长为. 16. 已知△ABC中,∠B=∠C=30°,AP⊥BC,垂足为P,AQ⊥AB交BC边于点Q.若△ABC的面积为4x2+y2 , △APQ的面积为 xy,则 的值为.
16. 已知△ABC中,∠B=∠C=30°,AP⊥BC,垂足为P,AQ⊥AB交BC边于点Q.若△ABC的面积为4x2+y2 , △APQ的面积为 xy,则 的值为.三、解答题
-
17. 计算:(1)、 +(-2019)0-( )-1;(2)、 × -( + )( - )18. 先化简,再求值: ,其中x=-2.19. 下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
请问:
(1)、该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果.(2)、请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.20. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF. 21. A、B两地相距80千米,一辆公共汽车从A地出发开往B地,2小时后,又从A地开来一辆小汽车,小汽车的速度是公共汽车的3倍.结果小汽车比公共汽车早40分钟到达B地.求两种车的速度.22. 如图,△ABC中,AB=2,BC= ,AC= .分别以A,C为圆心,大于 AC长为半径画弧,两弧分别交于点M,N.直线MN分别交AB,AC于点D,E.试求BD的长,
21. A、B两地相距80千米,一辆公共汽车从A地出发开往B地,2小时后,又从A地开来一辆小汽车,小汽车的速度是公共汽车的3倍.结果小汽车比公共汽车早40分钟到达B地.求两种车的速度.22. 如图,△ABC中,AB=2,BC= ,AC= .分别以A,C为圆心,大于 AC长为半径画弧,两弧分别交于点M,N.直线MN分别交AB,AC于点D,E.试求BD的长, 23. 已知实数x满足x4-1= x3- x(1)、试问x2能等于5吗?答:(填“能”或“不能”)(2)、求x2+ 的值.24. 如图,△ABC和△BED都是等腰直角三角形,∠ABC=∠DBE=90°,AD,CE相交于点G
23. 已知实数x满足x4-1= x3- x(1)、试问x2能等于5吗?答:(填“能”或“不能”)(2)、求x2+ 的值.24. 如图,△ABC和△BED都是等腰直角三角形,∠ABC=∠DBE=90°,AD,CE相交于点G (1)、求证:△ABD≌△CBE;(2)、求证:AD⊥CE;(3)、连接AE,CD,若AE= CD=5,求△ABC和△BED的面积之和.25. 我们规定:经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做该角形的“等周线”,“等周线”被这个三角形截得的线段叫做该三角形的“等周径”.例如等腰三角形底边上的中线即为它的“等周径”
(1)、求证:△ABD≌△CBE;(2)、求证:AD⊥CE;(3)、连接AE,CD,若AE= CD=5,求△ABC和△BED的面积之和.25. 我们规定:经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做该角形的“等周线”,“等周线”被这个三角形截得的线段叫做该三角形的“等周径”.例如等腰三角形底边上的中线即为它的“等周径” (1)、若等边三角形的“等周径”长为 ,则它的边长为;(2)、如图,点E为四边形ABCD的边AB上一点,已知∠DEC=∠A=∠B,AE=BC,过点E作EF⊥CD于点F,求证:直线EF为△DEC的“等周线”;(3)、Rt△ABC中,∠C=90°,AC=4,BC=3,若直线l为△ABC的“等周线”,请直接写出△ABC的所有“等周径”长.
(1)、若等边三角形的“等周径”长为 ,则它的边长为;(2)、如图,点E为四边形ABCD的边AB上一点,已知∠DEC=∠A=∠B,AE=BC,过点E作EF⊥CD于点F,求证:直线EF为△DEC的“等周线”;(3)、Rt△ABC中,∠C=90°,AC=4,BC=3,若直线l为△ABC的“等周线”,请直接写出△ABC的所有“等周径”长.