江苏省南京市玄武区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、0 B、1.010 010 001 C、π D、2. 已知a>0,b<0,那么点P(a,b)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,两个三角形是全等三角形,x的值是( )
 A、30 B、45 C、50 D、854. 下列函数中,y随x的增大而减小的有(
A、30 B、45 C、50 D、854. 下列函数中,y随x的增大而减小的有(①y=﹣2x+1;②y=6﹣x;③y=- ;④y=(1﹣ )x.
A、1个 B、2个 C、3个 D、4个5. 如图,动点P从点A出发,按顺时针方向绕半圆O匀速运动到点B,再以相同的速度沿直径BA回到点A停止,线段OP的长度d与运动时间t的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、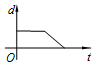 6. 如图,由四个全等的直角三角形拼成的图形,设CE= HG= 则斜边BD的长是( )
6. 如图,由四个全等的直角三角形拼成的图形,设CE= HG= 则斜边BD的长是( )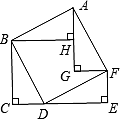 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 4的算术平方根是 , ﹣64的立方根是.8. 小明的体重为48.86kg,48.86≈.(精确到0.1)9. 如图,△ABC中,∠C=90°,D是BC上一点,∠1=∠2,CB=10,BD=6,则D到AB的距离为.
 10. 若直角三角形的两直角边长分别为5和12,则斜边上的中线长为 .11. 写出一个一次函数,使它的图象经过第一、三、四象限:.12. 将函数y=3x+1的图象平移,使它经过点(1,1),则平移后的函数表达式是 .13. 如图,长方形网格中每个小正方形的边长是1,△ABC是格点三角形(顶点都在格点上),则点C到AB的距离为.
10. 若直角三角形的两直角边长分别为5和12,则斜边上的中线长为 .11. 写出一个一次函数,使它的图象经过第一、三、四象限:.12. 将函数y=3x+1的图象平移,使它经过点(1,1),则平移后的函数表达式是 .13. 如图,长方形网格中每个小正方形的边长是1,△ABC是格点三角形(顶点都在格点上),则点C到AB的距离为. 14. 在平面直角坐标系xOy中,一次函数y=k1x+b(k1 , b均为常数)与正比例函数y=k2x(k2为常数)的图象如图所示,则关于x的不等式k2x<k1x+b的解集为.
14. 在平面直角坐标系xOy中,一次函数y=k1x+b(k1 , b均为常数)与正比例函数y=k2x(k2为常数)的图象如图所示,则关于x的不等式k2x<k1x+b的解集为. 15. 在平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(0,4).以点A为圆心,AB长为半径画弧,与x轴交于点C,则点C的坐标为.16. 如图,在长方形纸片ABCD中,AB=3,AD=9,折叠纸片ABCD,使顶点C落在边AD上的点G处,折痕分别交边AD、BC于点E、F,则△GEF的面积最大值是.
15. 在平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(0,4).以点A为圆心,AB长为半径画弧,与x轴交于点C,则点C的坐标为.16. 如图,在长方形纸片ABCD中,AB=3,AD=9,折叠纸片ABCD,使顶点C落在边AD上的点G处,折痕分别交边AD、BC于点E、F,则△GEF的面积最大值是.
三、解答题
-
17. 计算:18. 求x的值:(1)、(x+1)2=64(2)、8x3+27=0.19. 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
 (1)、求∠DAC的度数;(2)、求证:DC=AB.20. 如图,在平面直角坐标系xOy中,已知点A(﹣2,4),B(﹣5,4),C(﹣3,1),直线l经过点(1,0),且与y轴平行.
(1)、求∠DAC的度数;(2)、求证:DC=AB.20. 如图,在平面直角坐标系xOy中,已知点A(﹣2,4),B(﹣5,4),C(﹣3,1),直线l经过点(1,0),且与y轴平行. (1)、①请在图中画出△ABC;
(1)、①请在图中画出△ABC;②若△A1B1C1与△ABC关于直线l对称.请在图中画出△A1B1C1;
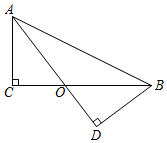
(2)、若点P(a,b)关于直线l的对称点为P1 , 则点P1的坐标是.21. 如图,在Rt△ACB和Rt△ADB中,∠C=∠D=90°,AD=BC,AD、BC相交于点O.求证:CO=DO.
 22. 客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,且部分对应关系如表所示.
22. 客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,且部分对应关系如表所示.x(kg)
…
30
40
50
…
y(元)
…
4
6
8
…
(1)、求y关于x的函数表达式;(2)、求旅客最多可免费携带行李的质量;(3)、当行李费2≤y≤7(元)时,可携带行李的质量x(kg)的取值范围是.23. 如图,在△ABC中,AB=6,AC=8,BC=10,BC的垂直平分线分别交AC、BC于点D、E,求CD的长. 24. 如图,在四边形ABCD中,AD∥BC,AD=2BC,点E是AD的中点,请仅用无刻度的直尺分别按下列要求画图.(不写画法,保留画图痕迹)
24. 如图,在四边形ABCD中,AD∥BC,AD=2BC,点E是AD的中点,请仅用无刻度的直尺分别按下列要求画图.(不写画法,保留画图痕迹) (1)、在图1中,画出△ACD的边AC上的中线DM;(2)、在图2中,若AC=AD,画出△ACD的边CD上的高AN.25. 甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发,甲、乙两人到达N地后均停止骑行.已知M、N两地相距 km,设甲行驶的时间为x(h),甲、乙两人之间的距离为y(km),表示y与x函数关系的部分图象如图所示.请你解决以下问题:
(1)、在图1中,画出△ACD的边AC上的中线DM;(2)、在图2中,若AC=AD,画出△ACD的边CD上的高AN.25. 甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发,甲、乙两人到达N地后均停止骑行.已知M、N两地相距 km,设甲行驶的时间为x(h),甲、乙两人之间的距离为y(km),表示y与x函数关系的部分图象如图所示.请你解决以下问题: (1)、求线段BC所在直线的函数表达式;(2)、求点A的坐标,并说明点A的实际意义;(3)、根据题目信息补全函数图象.(须标明相关数据)26.(1)、【初步探究】如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE、DE.判断△AED的形状,并说明理由.
(1)、求线段BC所在直线的函数表达式;(2)、求点A的坐标,并说明点A的实际意义;(3)、根据题目信息补全函数图象.(须标明相关数据)26.(1)、【初步探究】如图1,在四边形ABCD中,∠B=∠C=90°,点E是边BC上一点,AB=EC,BE=CD,连接AE、DE.判断△AED的形状,并说明理由. (2)、【解决问题】如图2,在长方形ABCD中,点P是边CD上一点,在边BC、AD上分别作出点E、F,使得点F、E、P是一个等腰直角三角形的三个顶点,且PE=PF,∠FPE=90°.要求:仅用圆规作图,保留作图痕迹,不写作法.
(2)、【解决问题】如图2,在长方形ABCD中,点P是边CD上一点,在边BC、AD上分别作出点E、F,使得点F、E、P是一个等腰直角三角形的三个顶点,且PE=PF,∠FPE=90°.要求:仅用圆规作图,保留作图痕迹,不写作法. (3)、【拓展应用】如图3,在平面直角坐标系xOy中,已知点A(2,0),点B(4,1),点C在第一象限内,若△ABC是等腰直角三角形,则点C的坐标是.
(3)、【拓展应用】如图3,在平面直角坐标系xOy中,已知点A(2,0),点B(4,1),点C在第一象限内,若△ABC是等腰直角三角形,则点C的坐标是. (4)、如图4,在平面直角坐标系xOy中,已知点A(1,0),点C是y轴上的动点,线段CA绕着点C按逆时针方向旋转90°至线段CB,CA=CB,连接BO、BA,则BO+BA的最小值是.
(4)、如图4,在平面直角坐标系xOy中,已知点A(1,0),点C是y轴上的动点,线段CA绕着点C按逆时针方向旋转90°至线段CB,CA=CB,连接BO、BA,则BO+BA的最小值是.