江苏省句容市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、 是有理数 B、5的平方根是 C、2< <3 D、数轴上不存在表示 的点3. 下列四组数,可作为直角三角形三边长的是( )A、 、 、 B、 、 、 C、 、 、 D、 、 、4. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
2. 下列说法正确的是( )A、 是有理数 B、5的平方根是 C、2< <3 D、数轴上不存在表示 的点3. 下列四组数,可作为直角三角形三边长的是( )A、 、 、 B、 、 、 C、 、 、 D、 、 、4. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )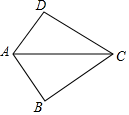 A、CB=CD B、∠BCA=∠DCA C、∠BAC=∠DAC D、∠B=∠D=90°5. 已知一次函数y=x+b的图像经过一、二、三象限,则b的值可以是A、-2 B、-1 C、0 D、26. 如图,数轴上的点 表示的数是-1,点 表示的数是1, 于点 ,且 ,以点 为圆心, 为半径画弧交数轴于点 ,则点 表示的数为( )
A、CB=CD B、∠BCA=∠DCA C、∠BAC=∠DAC D、∠B=∠D=90°5. 已知一次函数y=x+b的图像经过一、二、三象限,则b的值可以是A、-2 B、-1 C、0 D、26. 如图,数轴上的点 表示的数是-1,点 表示的数是1, 于点 ,且 ,以点 为圆心, 为半径画弧交数轴于点 ,则点 表示的数为( ) A、 B、 C、2.8 D、7. 如图,已知 平分 , 于 , , ,那么 ( )
A、 B、 C、2.8 D、7. 如图,已知 平分 , 于 , , ,那么 ( ) A、 B、 C、 D、8. 小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时 .小东骑自行车以 的速度直接回家,两人离家的路程 与各自离开出发地的时间 之间的函数图象如图所示,下列说法正确的有几个.( )
A、 B、 C、 D、8. 小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步,中途改为步行,到达图书馆恰好用时 .小东骑自行车以 的速度直接回家,两人离家的路程 与各自离开出发地的时间 之间的函数图象如图所示,下列说法正确的有几个.( )①家与图书馆之间的路程为 ;②小玲步行的速度为 ;③两人出发以后8分钟相遇;④两人出发以后 , 、 时相距 .
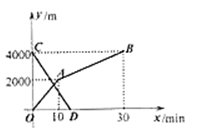 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. = .10. 比较大小:4 .(填“ ”,“ ”、“ ”)11. 若一个等腰三角形的顶角等于 ,则它底角等于 .12. 点 关于 轴对称点的坐标是.13. 用四舍五入法把圆周率 精确到千分位,得到的近似值是.14. 如图, ≌ ,若 , , ,则 的度数为.
 15. 如图,已知直线 与 的交点的横坐标为-2,则关于 的不等式 的解集为.
15. 如图,已知直线 与 的交点的横坐标为-2,则关于 的不等式 的解集为. 16. 如图,等腰 中, , 的垂直平分线 交边 于点 ,且 ,则 的度数是.
16. 如图,等腰 中, , 的垂直平分线 交边 于点 ,且 ,则 的度数是.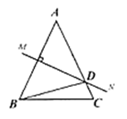 17. 一次函数 的图像经过的点的坐标如表格所示:
17. 一次函数 的图像经过的点的坐标如表格所示:…
-2
-1
0
1
…
…
0
2
4
6
…
当 时, 的取值范围是.
18. 已知点 在一次函数 的图像上,则 .19. 已知等腰 中, , , , 在线段 上, 是线段 上的动点, 的最小值是.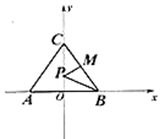 20. 如图,一次函数 的图像与 轴、 轴交于 、 两点, 是 轴上的一个动点,连接 ,将 沿 翻折,点 恰好落在 上,则点 的坐标为.
20. 如图,一次函数 的图像与 轴、 轴交于 、 两点, 是 轴上的一个动点,连接 ,将 沿 翻折,点 恰好落在 上,则点 的坐标为.
三、解答题
-
21. 计算(1)、(2)、(3)、在如图所示的 的正方形网格中画出一个 ,使 , , ,并求出 的面积.
 22. 如图, , , , ,求证: .
22. 如图, , , , ,求证: .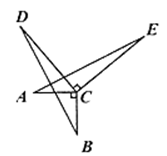 23. 已知:如图, , , 分别是 , 的中点.
23. 已知:如图, , , 分别是 , 的中点.求证: .
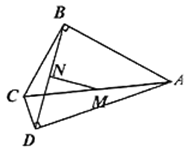 24. 如图,在 中,已知 , ,
24. 如图,在 中,已知 , ,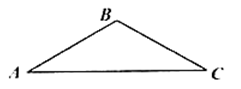 (1)、画 的垂直平分线 交 、 于点 、 (保留作图痕迹,作图痕迹请加黑描重);(2)、求 的度数;(3)、若 ,求 的长度.25. 学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形 中, , ,点 为 的中点, 和 相交于点 .求 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以 所在的直线为 轴,以 所在的直线为 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点 的坐标,从而求得 的面积.请你按照小明的思路解决这道思考题.
(1)、画 的垂直平分线 交 、 于点 、 (保留作图痕迹,作图痕迹请加黑描重);(2)、求 的度数;(3)、若 ,求 的长度.25. 学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形 中, , ,点 为 的中点, 和 相交于点 .求 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以 所在的直线为 轴,以 所在的直线为 轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点 的坐标,从而求得 的面积.请你按照小明的思路解决这道思考题.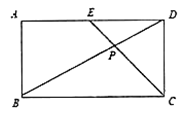 26. 甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶 ,先到终点的人原地休息.已知甲先出发 ,在整个过程中,甲、乙两车的距离 与甲出发的时间 之间的关系如图所示.
26. 甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶 ,先到终点的人原地休息.已知甲先出发 ,在整个过程中,甲、乙两车的距离 与甲出发的时间 之间的关系如图所示. (1)、甲的速度为 ,乙的速度为 ;(2)、说明 点表示的意义,求出 点坐标;(3)、求出线段 的函数关系式,并写出 的取值范围;(4)、甲出发多长时间两车相距 ,直接写出结果.27. 如图
(1)、甲的速度为 ,乙的速度为 ;(2)、说明 点表示的意义,求出 点坐标;(3)、求出线段 的函数关系式,并写出 的取值范围;(4)、甲出发多长时间两车相距 ,直接写出结果.27. 如图 (1)、【模型建立】如图1,等腰直角三角形 中, , ,直线 经过点 ,过 作 于点 ,过 作 于点 .求证: ;(2)、【模型应用】已知直线 : 与坐标轴交于点 、 ,将直线 绕点 逆时针旋转 至直线 ,如图2,求直线 的函数表达式;(3)、如图3,长方形 , 为坐标原点,点 的坐标为 ,点 、 分别在坐标轴上,点 是线段 上的动点,点 是直线 上的动点且在第四象限.若 是以点 为直角顶点的等腰直角三角形,请直接写出点 的坐标.
(1)、【模型建立】如图1,等腰直角三角形 中, , ,直线 经过点 ,过 作 于点 ,过 作 于点 .求证: ;(2)、【模型应用】已知直线 : 与坐标轴交于点 、 ,将直线 绕点 逆时针旋转 至直线 ,如图2,求直线 的函数表达式;(3)、如图3,长方形 , 为坐标原点,点 的坐标为 ,点 、 分别在坐标轴上,点 是线段 上的动点,点 是直线 上的动点且在第四象限.若 是以点 为直角顶点的等腰直角三角形,请直接写出点 的坐标.