江苏省常州市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列黑体大写英文字母中，不是轴对称图形的是 $($ $)$

A、T B、I C、N D、H

查看试题解析
2. 下列各点中位于第四象限的点是（）

A、（3，4） B、（﹣3，4） C、（3，﹣4） D、（﹣3，﹣4）

查看试题解析
3. 小亮的体重为47.95kg，用四舍五入法将47.95精确到0.1的近似值为（）

A、48 B、48.0 C、47 D、47.9

查看试题解析
4. 若一个三角形的三边长分别为3、4、5，则这个三角形最长边上的中线为（）

A、1.8 B、2 C、2.4 D、2.5

查看试题解析
5. 已知一次函数 $y = kx + b$ ，函数值y随自变量x的增大而减小，且 $kb > 0$ ，则函数 $y = kx + b$ 的图象大致是 $($ $)$

A、 B、 C、 D、

查看试题解析
6. 如图，点B、E、C、F在同一条直线上， $AB / / DE$ ， $AB = DE$ ，要用SAS证明 $△ ABC$ ≌ $△ DEF$ ，可以添加的条件是 $($ $)$

A、 $∠ A = ∠ D$ B、 $AC / / DF$ C、 $BE = CF$ D、 $AC = DF$

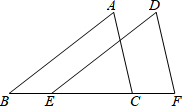查看试题解析
7. 如图，在 $△ ABC$ 中，AB、AC的垂直平分线分别交BC于点E、F，若 $∠ BAC = 112^{\circ}$ ，则 $∠ EAF$ 为 $($ $)$

A、 $38^{\circ}$ B、 $40^{\circ}$ C、 $42^{\circ}$ D、 $44^{\circ}$

查看试题解析
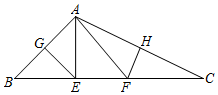8. 小苏和小林在如图①所示的跑道上进行 $4 \times 50$ 米折返跑.在整个过程中，跑步者距起跑线的距离 $y$ （单位： $m$ ）与跑步时间 $t$ （单位： $s$ ）的对应关系如图②所示.下列叙述正确的是（）.

A、两人从起跑线同时出发，同时到达终点 B、小苏跑全程的平均速度大于小林跑全程的平均速度 C、小苏前 $15 s$ 跑过的路程大于小林前 $15 s$ 跑过的路程 D、小林在跑最后 $100 m$ 的过程中，与小苏相遇2次

查看试题解析

二、填空题

9. 4的平方根为．

查看试题解析
10. 已知点 $P (- 3, 4)$ ，关于y轴对称的点的坐标为.

查看试题解析
11. 在实数 $\sqrt{16}$ ， $0.3$ ， $\sqrt{5}$ ， $\frac{2}{7}$ ， $- \frac{π}{2}$ 中，无理数有个 $.$

查看试题解析
12. 若点 $(m, m + 1)$ 在函数 $y = - \frac{1}{2} x + 2$ 的图象上，则 $m =$ .

查看试题解析
13. 下列关于建立平面直角坐标系的认识，合理的有.
$①$ 尽量使更多的点在坐标轴上； $②$ 尽量使图形关于坐标轴对称； $③$ 建立坐标系沟通了“数”与“形”之间的联系.

查看试题解析
14. 如图，在等边 $△ ABC$ 中，D、E分别是边AB、AC上的点，且 $AD = CE$ ，则 $∠ ADC + ∠ BEA =$ $^{\circ} .$

查看试题解析
15. 如图，在△ABC中，∠C＝90°，AD平分∠CAB，AC＝6，AD＝7，则点D到直线AB的距离是.

查看试题解析
16. 已知 $△ ABC$ 的三条边长分别为3，4，6，在 $△ ABC$ 所在平面内画一条直线，将 $△ ABC$ 分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画条 $.$

查看试题解析

三、解答题

17. 阅读理解：
$∵ \sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ， $∴ 1 < \sqrt{5} - 1 < 2$ .

$∴ \sqrt{5} - 1$ 的整数部分为1.

$∴ \sqrt{5} - 1$ 的小数部分为 $(\sqrt{5} - 1) - 1 = \sqrt{5} - 2$

解决问题：已知a是 $\sqrt{19} - 3$ 的整数部分，b是 $\sqrt{26} - 2$ 的小数部分，求 ${(- a)}^{3} + {(b + 5)}^{2}$ 的平方根.

查看试题解析
18. 如图（1）所示，在A，B两地间有一车站C，一辆汽车从A地出发经C站匀速驶往B地 $.$ 如图（2）是汽车行驶时离C站的路程 $y ($ 千米 $)$ 与行驶时间 $x ($ 小时 $)$ 之间的函数关系的图象.

(1)、填空： $a =$ km，AB两地的距离为km；

(2)、求线段PM、MN所表示的y与x之间的函数表达式；

(3)、求行驶时间x在什么范围时，小汽车离车站C的路程不超过60千米？

查看试题解析
19. 已知： $3 x^{2} = 12$ ，求x的值.

查看试题解析
20. 计算： $\sqrt{{(- 3)}^{2}} + {(3 - π)}^{0} - | 1 - \sqrt{2} | + \sqrt[3]{27}$ .

查看试题解析
21. 已知：如图，在 $△ ABC$ 中， $AB = AC$ ，BE、CD是中线 $.$ 求证： $BE = CD$ .

查看试题解析
22. 如图，点D是 $△ ABC$ 内部的一点， $BD = CD$ ，过点D作 $DE ⊥ AB$ ， $DF ⊥ AC$ ，垂足分别为E、F，且 $BE = CF .$
求证： $△ ABC$ 为等腰三角形.

查看试题解析

23. 请你用学习“一次函数”时积累的经验和方法研究函数

y = | x |

的图象和性质，并解决问题.

(1)、完成下列步骤，画出函数

y = | x |

的图象；

①列表、填空；

x	$\dots$	$- 3$	$- 2$	$- 1$	0	1	2	3	$\dots$
y	$\dots$	3		1		1	2	3	$\dots$

②描点：

③连线

(2)、观察图象，当x时，y随x的增大而增大；

(3)、结合图象，不等式

| x | < x + 2

的解集为.

查看试题解析

24. 某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如表：

x/元

…

15

20

25

…

y/件

…

25

20

15

…

已知日销售量y是销售价x的一次函数．

(1)、求日销售量y（件）与每件产品的销售价x（元）之间的函数表达式；

(2)、当每件产品的销售价定为35元时，此时每日的销售利润是多少元？

查看试题解析
25. 如图

(1)、问题解决：①如图1，在平面直角坐标系xOy中，一次函数 $y = \frac{1}{4} x + 1$ 与x轴交于点A，与y轴交于点B，以AB为腰在第二象限作等腰直角 $△ ABC$ ， $∠ BAC = 90^{\circ}$ ，点A、B的坐标分别为A、B.
②求①中点C的坐标.小明同学为了解决这个问题，提出了以下想法：过点C向x轴作垂线交x轴于点 $D .$ 请你借助小明的思路，求出点C的坐标；

(2)、类比探究：数学老师表扬了小明同学的方法，然后提出了一个新的问题，如图2，在平面直角坐标系xOy中，点A坐标 $(0 ， - 6)$ ，点B坐标 $(8 ， 0)$ ，过点B作x轴垂线l，点P是l上一动点，点D是在一次函数 $y = - 2 x + 2$ 图象上一动点，若 $△ APD$ 是以点D为直角顶点的等腰直角三角形，请直接写出点D与点P的坐标.

查看试题解析

x/元	…	15	20	25	…
y/件	…	25	20	15	…