江苏省滨海县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-08 类型:期末考试
一、单选题
-
1. 在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点P(-3.2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列实数中,无理数是A、 B、 C、 D、4. 下列各组数中,是勾股数的是A、1、2、3 B、3、4、5 C、12、15、18 D、1、 、35. 下列一次函数中,y随x增大而增大的是A、 B、 C、 D、6. 下列条件中,不能判定两个三角形全等的是A、两边及其夹角分别相等 B、两角及其夹边分别相等 C、三个角分别相等 D、三边分别相等7. 到三角形三条边距离相等的点是( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点8. 等腰三角形周长为20cm,底边长ycm与腰长xcm之间的函数关系是 )A、 B、 C、 D、
2. 在平面直角坐标系中,点P(-3.2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列实数中,无理数是A、 B、 C、 D、4. 下列各组数中,是勾股数的是A、1、2、3 B、3、4、5 C、12、15、18 D、1、 、35. 下列一次函数中,y随x增大而增大的是A、 B、 C、 D、6. 下列条件中,不能判定两个三角形全等的是A、两边及其夹角分别相等 B、两角及其夹边分别相等 C、三个角分别相等 D、三边分别相等7. 到三角形三条边距离相等的点是( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点8. 等腰三角形周长为20cm,底边长ycm与腰长xcm之间的函数关系是 )A、 B、 C、 D、二、填空题
-
9. 使 有意义的x的取值范围是 .10. 等腰三角形的一个内角120°,则它的底角是
11. 点P(﹣4,2)关于x轴对称的点Q的坐标.12. 将函数 的图象向上平移3个单位,得到的图象的函数表达式为.13. 地球上七大洲的总面积约为149480000km2 , 用科学记数法表示为 km2 . (精确到10000000)14. 如图, ≌ , , ,则 . 15. 如图, 中,边AB的垂直平分线分别交AB、BC于点D、E,连接 若 , ,则 的周长为.
15. 如图, 中,边AB的垂直平分线分别交AB、BC于点D、E,连接 若 , ,则 的周长为.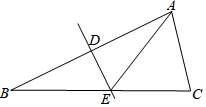 16. 若一次函数 、 的图象相交于 ,则关于x、y的方程组 的解为.17. 一次函数 的图象如图所示,则一元一次不等式 的解集为.
16. 若一次函数 、 的图象相交于 ,则关于x、y的方程组 的解为.17. 一次函数 的图象如图所示,则一元一次不等式 的解集为.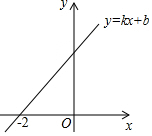 18. 如图,在平面直角坐标系中,点B在x轴上, 是等边三角形, ,则点A的坐标为.
18. 如图,在平面直角坐标系中,点B在x轴上, 是等边三角形, ,则点A的坐标为.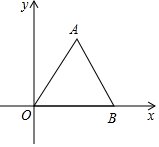
三、解答题
-
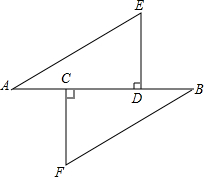
19. 求x的值:(1)、 ;(2)、 ;20.(1)、 ;(2)、 .21. 已知:如图, , ,垂足分别为D、C, ,且 求证: ≌ .
 22. 如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
22. 如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
①在网格中,画出这个平面直角坐标系;
②在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.
23. 如图,在 中,CD是斜边AB上的中线, ,垂足为E (1)、如果 , ,那么 cm, cm:(2)、求证: .24. 如图,直线 : 与直线 : 相交于点 .
(1)、如果 , ,那么 cm, cm:(2)、求证: .24. 如图,直线 : 与直线 : 相交于点 . (1)、求b和m的值;(2)、结合图象,直接写出当 时x的取值范围.25. 2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程 与时间 的函数图象 请根据
(1)、求b和m的值;(2)、结合图象,直接写出当 时x的取值范围.25. 2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程 与时间 的函数图象 请根据图中的信息,解答下列问题:
 (1)、根据图象信息,普通列车比动车早出发h,动车的平均速度是 ;(2)、分别求出OA、BC的函数表达式,并写出自变量x的取值范围;(3)、动车出发多少小时追上普通列车?此时他们距离出发地多少千米?26. 如图,点A、B、C在一条直线上,分别以AB、AC为腰,在BC的同侧作等腰三角形,使 , ,BE、CD交于点P,BE与AD、CD与AE分别交于点M、N.
(1)、根据图象信息,普通列车比动车早出发h,动车的平均速度是 ;(2)、分别求出OA、BC的函数表达式,并写出自变量x的取值范围;(3)、动车出发多少小时追上普通列车?此时他们距离出发地多少千米?26. 如图,点A、B、C在一条直线上,分别以AB、AC为腰,在BC的同侧作等腰三角形,使 , ,BE、CD交于点P,BE与AD、CD与AE分别交于点M、N. (1)、如图,若 .
(1)、如图,若 .①求证: ≌ ;②求 的度数;
(2)、如图,若 ,则BE与CD间的数量关系为 , 的大小为 用含 的代数式表示27. 如图,在平面直角坐标系中,直线 : 与直线 : 交于点 ,与y轴交于点 ,与x轴交于点C. (1)、求直线 的函数表达式;(2)、求 的面积;(3)、在平面直角坐标系中有一点 ,使得 ,请求出点P的坐标;(4)、点M为直线 上的动点,过点M作y轴的平行线,交 于点N,点Q为y轴上一动点,且 为等腰直角三角形,请直接写出满足条件的点M的坐标.
(1)、求直线 的函数表达式;(2)、求 的面积;(3)、在平面直角坐标系中有一点 ,使得 ,请求出点P的坐标;(4)、点M为直线 上的动点,过点M作y轴的平行线,交 于点N,点Q为y轴上一动点,且 为等腰直角三角形,请直接写出满足条件的点M的坐标.