湖北省孝感市云梦县2016-2017学年七年级下学期期末考试数学试题
试卷更新日期:2017-08-03 类型:期末考试
一、选择题
-
1. 9的算术平方根是( )A、3 B、 C、 D、2. 下列各图中,∠1和∠2是对顶角的是( )A、
 B、
B、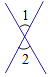 C、
C、 D、
D、 3. 在平面直角坐标系中,点P(6,-10)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 二元一次方程组 的解是( )A、 B、 C、 D、5. 若 ,则下列不等式不正确的是( )A、 B、 C、 D、6. 要调查下列问题,适合采用全面调查的是( )A、检测云梦县的空气质量 B、孝武超市招聘,对应聘人员进行面试 C、调查云梦县小学生的视力和用眼卫生情况 D、检测梦泽鞋厂生产的鞋底能承受的弯折次数7. 下列图案,分别是奥迪、奔驰、三菱、大众汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )A、
3. 在平面直角坐标系中,点P(6,-10)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 二元一次方程组 的解是( )A、 B、 C、 D、5. 若 ,则下列不等式不正确的是( )A、 B、 C、 D、6. 要调查下列问题,适合采用全面调查的是( )A、检测云梦县的空气质量 B、孝武超市招聘,对应聘人员进行面试 C、调查云梦县小学生的视力和用眼卫生情况 D、检测梦泽鞋厂生产的鞋底能承受的弯折次数7. 下列图案,分别是奥迪、奔驰、三菱、大众汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )A、 B、
B、 C、
C、 D、
D、 8.
8.如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
 A、∠1=∠2 B、∠3=∠4 C、∠C=∠CDE D、∠C+∠CDA=180°9. 下列命题中,假命题是( )A、如果两条直线都与第三条直线平行,那么这两条直线也互相平行 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、两条直线被第三条直线所截,同旁内角互补 D、两直线平行,内错角相等10. 体育委员统计了七(1)班全体同学60秒跳绳的次数,并列出下面的频数分布表:
A、∠1=∠2 B、∠3=∠4 C、∠C=∠CDE D、∠C+∠CDA=180°9. 下列命题中,假命题是( )A、如果两条直线都与第三条直线平行,那么这两条直线也互相平行 B、在同一平面内,过一点有且只有一条直线与已知直线垂直 C、两条直线被第三条直线所截,同旁内角互补 D、两直线平行,内错角相等10. 体育委员统计了七(1)班全体同学60秒跳绳的次数,并列出下面的频数分布表:次数
60≤x<80
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
频数
2
4
21
14
7
3
1
给出以下结论:①全班有52个学生; ②组距是20; ③组数是7;④跳绳次数在100≤x<140范围的学生约占全班学生的67%.其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 的立方根是.
12. 《孙子算经》是中国重要的古代数学著作.书中记载了有趣的“鸡兔同笼”问题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这句话的意思是:“有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?”设有鸡x只,兔y只,可列方程组为.13. 一个三位数,十位、百位上的数的和等于个位上的数,百位上的数的6倍等于个位、十位上的数的和,且个位、十位、百位上的数的和是14,则这个三位数是.14. 不等式组 的解集是 ,则关于 的方程 的解为.15.如图,若∠1=∠D=38°,∠C和∠D互余,则∠B =.
 16.
16.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),……,依此规律跳动下去,点A第2018次跳动至点A2018的坐标是.

三、解答题
-
17. 化简或计算:(1)、;
(2)、18. 解下列二元一次方程组:
(1)、;
(2)、
19. 解下列不等式组,并把它们的解集表示在数轴上.(1)、;
(2)、
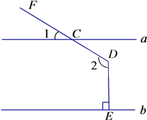
20.如图,直线a∥b , 射线DF与直线a相交于点C , 过点D作DE⊥b于点E , 已知∠1=30°,求∠2的度数.
 21.
21.如图,D是AB延长线上一点,AE平分∠BAC , ∠BAC=∠C=∠CBE.
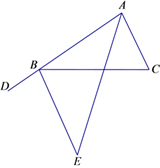 (1)、求证:BE平分∠DBC(2)、求证:∠E=∠BAE22.
(1)、求证:BE平分∠DBC(2)、求证:∠E=∠BAE22.小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组
频数
百分比
600≤x<800
2
5%
800≤x<1000
6
15%
1000≤x<1200
a
40%
1200≤x<1400
9
22.5%
1400≤x<1600
b
c
1600≤x<1800
2
5%
合计
40
100%
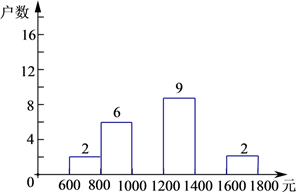
根据以上提供的信息,解答下列问题:
(1)、频数分布表中:a= , b= , c= .(2)、补全频数分布直方图.(3)、请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?23. 某电视机厂生产甲、乙、丙三种不同型号的电视机,出厂价分别为1200元,2000元,2200元.某商场同时从该厂购进其中两种不同型号的电视机共50台,正好用去80000元.(1)、该商场有几种进货方案?(写出演算步骤)(2)、若该商场销售甲、乙、丙种电视机每台可分别获利200元,250元,300元,如何进货可使销售时获利最大?最大利润是多少?24.如图,在平面直角坐标系中,点 的坐标分别为(1,0)、(-2,0),现同时将点 分别向上平移2个单位,再向左平移1个单位,分别得到点 的对应点 ,连接 、 、 .
 (1)、若在 轴上存在点 ,连接 ,使S△ABM=S□ABDC , 求出点 的坐标;(2)、若点 在线段 上运动,连接 ,求S=S△PCD+S△POB的取值范围;(3)、若 在直线 上运动,请直接写出 的数量关系.
(1)、若在 轴上存在点 ,连接 ,使S△ABM=S□ABDC , 求出点 的坐标;(2)、若点 在线段 上运动,连接 ,求S=S△PCD+S△POB的取值范围;(3)、若 在直线 上运动,请直接写出 的数量关系.