2017年天津市南开区高考数学模拟试卷（理科）（5月份）

试卷更新日期：2017-08-02 类型：高考模拟

进入出卷网下载

一、选择题

1. 设复数z₁ ， z₂在复平面内的对应点关于虚轴对称，z₁=1+2i，i为虚数单位，则z₁z₂=（）

A、1﹣2i B、5i C、﹣5 D、5

查看试题解析
2. 函数f（x）=2^x+x³﹣2在区间（0，1）内的零点个数是（）

A、0 B、1 C、2 D、3

查看试题解析
3. 若x，y∈R，则“x²＞y²”是“x＞y”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 在如图所示的程序框图中，若输出的值是3，则输入x的取值范围是（）

A、（4，10] B、（2，+∞） C、（2，4] D、（4，+∞）

查看试题解析
5. 在区间 $[0 ， \frac{π}{2}]$ 上任选两个数x和y，则y＜sinx的概率为（）

A、 $\frac{2}{π^{2}}$ B、 $1 - \frac{4}{π^{2}}$ C、 $\frac{4}{π^{2}}$ D、 $1 - \frac{2}{π^{2}}$

查看试题解析
6. 一个几何体的三视图如图所示，该几何体的表面积为（）

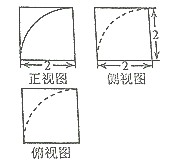A、24﹣π B、24﹣3π C、24+π D、24﹣2π

查看试题解析
7. 已知等差数列{a_n}的前n项和为s_n ，且S₂=10，S₅=55，则过点P（n，a_n），Q（n+2，a_n₊₂）（n∈N^*）的直线的斜率为（）

A、4 B、 $\frac{1}{4}$ C、﹣4 D、﹣ $\frac{1}{4}$

查看试题解析
8. 已知函数f（x）=﹣ $\frac{π}{2 x}$ ，g（x）=xcosx﹣sinx，当x∈[﹣3π，3π]时，方程f（x）=g（x）根的个数是（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

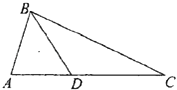
9. 某人5次下班途中所花的时间（单位：分钟）分别为m，n，5，6，4．已知这组数据的平均数为5，方差为2，则|m﹣n|的值为．

查看试题解析
10. （x﹣ $\frac{2}{x}$ ）ⁿ的展开式中只有第5项的二项式系数最大，则它的展开式中常数项是．

查看试题解析
11. 已知向量 $\vec{a}$ ， $\vec{b}$ ，| $\vec{a}$ |= $\sqrt{3}$ ，| $\vec{b}$ |=2，（ $\vec{a}$ + $\vec{b}$ ）⊥ $\vec{a}$ ，则向量 $\vec{a}$ ， $\vec{b}$ 的夹角为．

查看试题解析
12. 如图，在△ABC中，D是边AC上的点，且 $A B = A D ， 2 A B = \sqrt{3} B D ， B C = 2 B D$ ，则sinC的值为．

查看试题解析
13. 过点（0，3b）的直线l与双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的一条斜率为正值的渐近线平行，若双曲线C的右支上的点到直线l的距离恒大于b，则双曲线C的离心率的最大值是．

查看试题解析
14. 若a＞0，b＞0，且2a+b=1，则2 $\sqrt{a b}$ ﹣4a²﹣b²的最大值是．

查看试题解析

三、解答题

15. 设函数f（x）= $\frac{\sqrt{2}}{2}$ cos（2x+ $\frac{π}{4}$ ）+sin²x．

(1)、求函数f（x）的最小周期；

(2)、设函数g（x）对任意x∈R，有g（x+ $\frac{π}{2}$ ）=g（x），且当x∈[0， $\frac{π}{2}$ ]时，g（x）= $\frac{1}{2}$ ﹣f（x）．求函数g（x）在[﹣π，0]上的解析式．

查看试题解析
16. 某仪器经过检验合格才能出厂，初检合格率为 $\frac{3}{4}$ ：若初检不合格，则需要进行调试，经调试后再次对其进行检验；若仍不合格，作为废品处理，再检合格率为 $\frac{4}{5}$ ．每台仪器各项费用如表：
项目
生产成本
检验费/次
调试费
出厂价
金额（元）
1000
100
200
3000
（Ⅰ）求每台仪器能出厂的概率；
（Ⅱ）求生产一台仪器所获得的利润为1600元的概率（注：利润=出厂价﹣生产成本﹣检验费﹣调试费）；
（Ⅲ）假设每台仪器是否合格相互独立，记X为生产两台仪器所获得的利润，求X的分布列和数学期望．

查看试题解析
17.
如图，四棱锥P﹣ABCD中，侧面PDC是正三角形，底面ABCD是边长为2 $\sqrt{3}$ 的菱形，∠DAB=120°，且侧面PDC与底面垂直，M为PB的中点．
（Ⅰ）求证：PA⊥平面CDM
（Ⅱ）求二面角D﹣MC﹣A的余弦值．

查看试题解析
18. 已知数列{a_n}的前n项和为S_n ，且2S_n=1﹣a_n（n∈N^*）．

（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n= $\frac{1}{l o g_{\frac{1}{3}} a_{n}}$ ，c_n= $\frac{\sqrt{b_{n} b_{n + 1}}}{\sqrt{n + 1} + \sqrt{n}}$ ，求数列{c_n}的前n项和T_n ．

查看试题解析
19. 已知x=1是函数f（x）=mx³﹣3（m+1）x²+nx+1的一个极值点，其中m，n∈R，m＜0．

（Ⅰ）求m与n的关系表达式；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）当x∈[﹣1，1]时，函数y=f（x）的图象上任意一点的切线斜率恒大于3m，求m的取值范围．

查看试题解析
20.
已知椭圆 $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率为 $\frac{\sqrt{2}}{2}$ ，且过点（2， $\sqrt{2}$ ）．

(1)、求椭圆的标准方程；

(2)、四边形ABCD的顶点在椭圆上，且对角线AC、BD过原点O，若k_AC•k_BD=﹣ $\frac{b^{2}}{a^{2}}$ ，
（i）求 $\vec{O A}$ • $\vec{O B}$ 的最值；
（ii）求证：四边形ABCD的面积为定值．

查看试题解析

项目	生产成本	检验费/次	调试费	出厂价
金额（元）	1000	100	200	3000