初中数学北师大版九年级下学期 第一章 1.1 锐角三角函数
试卷更新日期:2020-01-06 类型:同步测试
一、单选题
-
1. 如图,在Rt△ABC中,∠C=90°,若AB=5,AC=4,则cosB的值( )
 A、 B、 C、 D、2. 如图,在 中, ,则 的值是( )
A、 B、 C、 D、2. 如图,在 中, ,则 的值是( )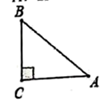 A、 B、 C、 D、3. 如图,在平面直角坐标系中,点 的坐标为 ,那么 的值是( )
A、 B、 C、 D、3. 如图,在平面直角坐标系中,点 的坐标为 ,那么 的值是( )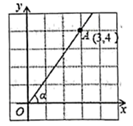 A、 B、 C、 D、4. 直线 与y轴相交,所成的锐角的正切值为 ,则k的值为( )A、 B、 C、 D、无法确定5. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
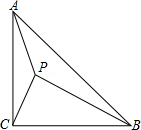
A、 B、 C、 D、4. 直线 与y轴相交,所成的锐角的正切值为 ,则k的值为( )A、 B、 C、 D、无法确定5. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )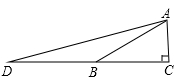 A、 B、2 C、 D、36. 如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,连结CD与AB相交于点P,则tan∠APD的值是( )
A、 B、2 C、 D、36. 如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,连结CD与AB相交于点P,则tan∠APD的值是( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
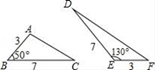
7. 在Rt△ABC中,∠C=90°,BC=6,AC=8,则cosB的值是 .8. 如图,若△ABC和△DEF的面积分别为S1 、S2 , 则S1与S2 的数量关系为.
三、解答题
-
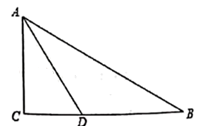
9. 如图,在 中, ,点 在边 上, 求 的值。
四、综合题