河北省保定市高阳县2016-2017学年七年级下学期期末考试数学试卷

试卷更新日期：2017-08-02 类型：期末考试

进入出卷网下载

一、选择题

1. 点P（5，3）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 4的平方根是（）

A、2 B、± 2 C、16 D、±16

查看试题解析
3. 若 $a > b$ ，则下列不等式正确的是（）

A、 $3 a < 3 b$ B、 $m a > m b$ C、 $- a - 1 > - b - 1$ D、 $\frac{a}{2} + 1 > \frac{b}{2} + 1$

查看试题解析
4. 下列调查中，调查方式选择合理的是（）

A、为了了解某一品牌家具的甲醛含量，选择全面调查； B、为了了解神舟飞船的设备零件的质量情况，选择抽样调查； C、为了了解某公园全年的游客流量，选择抽样调查； D、为了了解一批袋装食品是否含有防腐剂，选择全面调查.

查看试题解析
5.
如右图，数轴上点P 表示的数可能是（）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、 $\sqrt{10}$ D、 $\sqrt{15}$

查看试题解析
6.
如图，能判定AB∥CD的条件是（）

A、∠1=∠2 B、∠3=∠4 C、∠1=∠3 D、∠2=∠4

查看试题解析
7. 下列说法正确的是（）

A、 $- (- 8)$ 的立方根是-2 B、立方根等于本身数有 $- 1 ， 0 ， 1$ C、 $- \sqrt{64}$ 的立方根为-4 D、一个数的立方根不是正数就是负数

查看试题解析
8. 如图，直线l₁ ， l₂ ， l₃交于一点，直线l₄∥l₁ ，若∠1=124°，∠2=88°，则∠3的度数为（）

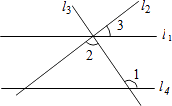A、26° B、36° C、46° D、56°

查看试题解析
9. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} a x + b y = 7 \\ a x - b y = 1 \end{matrix}$ 的解，则 $a - b$ 的值为（）

A、3 B、2 C、1 D、－1

查看试题解析
10.
在如图的方格纸上，若用（-1，1）表示A点，（0，3）表示B点，那么C点的位置可表示为（）

A、（1，2） B、（2，3） C、（3，2） D、（2，1）

查看试题解析
11. 若不等式组 ${\begin{matrix} 2 x - 1 > 3 \\ x \leq a \end{matrix}$ 的整数解共有三个，则a的取值范围是（）

A、 $5 \leq a < 6$ B、 $5 < a \leq 6$ C、 $5 < a < 6$ D、 $5 \leq a \leq 6$

查看试题解析
12.
运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是（　　）

A、x≥11 B、11≤x＜23 C、11＜x≤23 D、x≤23

查看试题解析

二、填空题

13. 不等式 $\frac{x - 2}{3} \leq 1$ 的解集是；

查看试题解析
14. 若 ${\begin{matrix} x = a \\ y = b \end{matrix}$ 是方程 $2 x + y = 0$ 的一个解，则 $6 a + 3 b - 2$ =；

查看试题解析
15. 已知线段MN平行于x轴，且MN的长度为5，若M的坐标为（2，-2），那么点N的坐标是；

查看试题解析
16.
如图，若∠1=∠D=39°，∠C=51°，则∠B=°；

查看试题解析
17. 已知5x-2的立方根是-3，则x+69的算术平方根是；

查看试题解析
18. 在平面直角坐标系中，如果一个点的横、纵坐标均为整数，那么我们称该点为整点，若整点P（ $m + 2$ ， $\frac{1}{2} m - 1$ ）在第四象限，则m的值为；

查看试题解析
19. 已知方程组 ${\begin{matrix} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{matrix}$ 由于甲看错了方程①中的a得到方程组的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ；乙看错了方程②中的b得到方程组的解为 ${\begin{matrix} x = 5 \\ y = 4 \end{matrix}$ ，若按正确的a、b计算,则原方程组的解为；

查看试题解析
20. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”如果设木条长x尺，绳子长y尺，可列方程组为；

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt[3]{- 27} - \sqrt{3^{2}} - \sqrt{{(- 1)}^{2}} + \sqrt[3]{8}$

(2)、 $| 1 - \sqrt{2} | - | \sqrt{3} - \sqrt{2} |$

查看试题解析
22. 计算：

(1)、解方程组： ${\begin{matrix} x - y = 13 \\ x = 6 y - 7 \end{matrix}$

(2)、解不等式组： ${\begin{matrix} 5 x - 9 < 3 (x - 1) \\ 1 - \frac{3}{2} x \leq \frac{1}{2} x - 1 \end{matrix}$

查看试题解析
23.
某校随机抽取部分学生，就“学习习惯”进行调查，将“对自己做错题进行整理、分析、改正”（选项为：很少、有时、常常、总是）的调查数据进行了整理，绘制成部分统计图如下：
请根据图中信息，解答下列问题：

(1)、该调查的样本容量为， $a$ =%， $b$ =%，“常常”对应扇形的圆心角的度数为；

(2)、请你补全条形统计图；

(3)、若该校有3200名学生，请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名？

查看试题解析
24.
如图，在平面直角坐标系中，已知长方形ABCD的两个顶点坐标为A（2，-1），C（6，2），点M为y轴上一点，△MAB的面积为6，且MD＜MA；
请解答下列问题：

(1)、顶点B的坐标为；

(2)、求点M的坐标；

(3)、在△MAB中任意一点P（ $x_{0}$ ， $y_{0}$ ）经平移后对应点为 $P_{1}$ （ $x_{0}$ -5， $y_{0}$ -1），将△MAB作同样的平移得到△ $M_{1} A_{1} B_{1}$ ，则点 $M_{1}$ 的坐标为。

查看试题解析
25.
课上教师呈现一个问题
甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如下图：
甲同学辅助线的做法和分析思路如下：

(1)、请你根据乙同学所画的图形，描述辅助线的做法，并写出相应的分析思路.

(2)、请你根据丙同学所画的图形，求∠EFG的度数．

查看试题解析
26.
对于有理数a ， b ，定义min 的含义为：当a≥b时，min ＝b；当a＜b时，min ＝a.
例如：min ＝－2，min ${- 3 ， - 3}$ ＝-3.

(1)、min ${- 1 ， 2}$ =；

(2)、求min{x²＋1，0}；

(3)、已知min{－2k＋5，－1}＝－1，求k的取值范围；

(4)、已知min{ $5 - {(m - 1)}^{2} - {(n + 2)}^{2}$ ，5}＝5，直接写出m ， n的值．

查看试题解析
27. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，下表是近两周的销售情况：
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
（进价、售价均保持不变，利润=销售收入﹣进货成本）

(1)、求A、B两种型号的电风扇的销售单价；

(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？

(3)、在（2）的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．

查看试题解析

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	4台	1200元
第二周	5台	6台	1900元