江苏省泰兴市2016-2017学年七年级下学期期末考试数学试题
试卷更新日期:2017-08-02 类型:期末考试
一、选择题
-
1. 下列图形中,由 ,能得到 的是( )A、
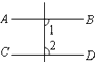 B、
B、 C、
C、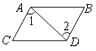 D、
D、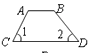 2.
2.在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
 A、120° B、110° C、100° D、90°3. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点A,点C分别在直线a,b上,且a∥b.若∠1=60°,则∠2的度数为( )
A、120° B、110° C、100° D、90°3. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点A,点C分别在直线a,b上,且a∥b.若∠1=60°,则∠2的度数为( )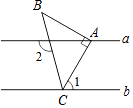 A、75° B、105° C、135° D、155°4. 有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A、75° B、105° C、135° D、155°4. 有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A、 B、 C、 D、5. 能说明“对于任何实数a, ”是假命题的一个反例可以是 ( )A、 B、 C、 D、6.如图,AD是△ABC的中线,DE是△ADC的高线,AB=3,AC=5,DE=2,点D到AB的距离是( )
 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
7. 直接写出计算结果: =; .8. 若把代数式 化成 的形式,其中m , k为常数,则 = .9.
如图,正方形ABCD是由两个小正方形和两个小长方形组成的,根据图形写出一个正确的等式:.
 10.
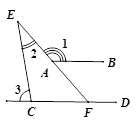
10.如图,AB∥CD , 则∠1+∠3—∠2的度数等于 .
 11. 已知 ,且 ,那么 的值为 .12.
11. 已知 ,且 ,那么 的值为 .12.已知 则第
 个等式为 . 13. 如果∠A与∠B的两边分别平行,∠A比∠B的3倍少36°,则∠A的度数是.
个等式为 . 13. 如果∠A与∠B的两边分别平行,∠A比∠B的3倍少36°,则∠A的度数是.
14.已知关于
 的不等式组 只有两个整数解,则
的不等式组 只有两个整数解,则 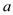 的取值范围.15. 某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有块.16. 以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是.(填序号)
的取值范围.15. 某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有块.16. 以下四个命题:①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;②三角形的三条高所在的直线的交点可能在三角形的内部或外部;③多边形的所有内角中最多有3个锐角;④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.其中真命题的是.(填序号)三、解答题
-
17. 计算:(1)、;
(2)、
18. 把下列各式分解因式:(1)、;
(2)、
19. 已知x,y满足方程组 ,求代数式 的值.20. 综合题:
(1)、完成下面的推理说明:
已知:如图, ∥ , 、 分别平分 和 .

求证: ∥ .
证明: 、 分别平分 和 (已知),
, ( ).
∥ ( ),
().
().
(等式的性质).
∥ ( ).
(2)、说出(1)的推理中运用了哪两个互逆的真命题.21. 解下列方程组或不等式(组):(1)、解方程组(2)、解不等式组 ,并把解集在数轴上表示出来.22.如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
 (1)、△ABC的面积为;(2)、将△ABC经过平移后得到△A′B′C′ , 图中标出了点B的对应点B′ , 补全△A′B′C′;(3)、若连接AA′ , BB′ , 则这两条线段之间的关系是;(4)、在图中画出△ABC的高CD .23.
(1)、△ABC的面积为;(2)、将△ABC经过平移后得到△A′B′C′ , 图中标出了点B的对应点B′ , 补全△A′B′C′;(3)、若连接AA′ , BB′ , 则这两条线段之间的关系是;(4)、在图中画出△ABC的高CD .23.如图,∠ABD和∠BDC的平分线相交于点E , BE交CD于点F , ∠1+∠2=90°.试问直线AB , CD在位置上有什么关系?∠2与∠3在数量上有什么关系?并证明你的猜想.
 24.
24.某商场销售A , B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
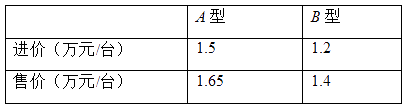
该商场计划购进两种教学设备若干台,共需66万元,全部销售后可获毛利润9万元.
(毛利润=(售价 - 进价)×销售量)
(1)、该商场计划购进A , B两种品牌的教学设备各多少台?(2)、通过市场调研,该商场决定在原计划的基础上,减少A型设备的购进数量,增加B型设备的购进数量,已知B型设备增加的数量是A型设备减少数量的1.5倍.若用于购进这两种型号教学设备的总资金不超过68.7万元,问A型设备购进数量至多减少多少台?25.已知如图,∠COD=90°,直线AB与OC交于点B , 与OD交于点A , 射线OE与射线AF交于点G.
 (1)、若OE平分∠BOA , AF平分∠BAD , ∠OBA=42°,则∠OGA=;(2)、若∠GOA= ∠BOA , ∠GAD= ∠BAD , ∠OBA=42°,则∠OGA=;
(1)、若OE平分∠BOA , AF平分∠BAD , ∠OBA=42°,则∠OGA=;(2)、若∠GOA= ∠BOA , ∠GAD= ∠BAD , ∠OBA=42°,则∠OGA=;
(3)、将(2)中的“∠OBA=42°”改为“∠OBA= ”,其它条件不变,求∠OGA的度数.(用含 的代数式表示)(4)、若OE将∠BOA分成1︰2两部分,AF平分∠BAD , ∠ABO= (30°< α <90°) ,求∠OGA的度数.(用含 的代数式表示)