湖北省荆州市松滋市2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-03 类型：期末考试

进入出卷网下载

一、单选题

1. 用配方法解方程x²-4x+1=0时，配方后所得的方程是（　　）

A、（x-2）²=1 B、（x-2）²=-1 C、（x-2）²=3 D、（x+2）²=3

查看试题解析
2. 方程x²﹣5x﹣1＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
3. 已知m是方程x²﹣2x﹣2019＝0的一个根，则2m²﹣4m的值等于（）

A、2019 B、﹣2019 C、4038 D、﹣4038

查看试题解析
4. 三角形的两边长分别为3和6，第三边长为方程x²﹣7x+10＝0的一个根，则这个三角形的周长为（）

A、11 B、11或14 C、16 D、14

查看试题解析
5. 已知⊙O的半径为2，直线l上有一点P满足PO=2，则直线l与⊙O的位置关系是( )
　

A、相切 B、相离 C、相离或相切 D、相切或相交

查看试题解析
6. 反比例函数y＝ $\frac{k - 1}{x}$ 的图象位于第二、四象限，则k的取值范围是（）

A、k≥1 B、k＞1 C、k＜1 D、k≤1

查看试题解析
7. 已知抛物线y＝﹣2（x+1）²+3，则下列说法，错误的是（）

A、开口方向向下 B、当x＜﹣1时，y随x的增大而减小 C、对称轴是直线x＝﹣1 D、顶点坐标是（﹣1，3）

查看试题解析
8. 已知抛物线y=x²+bx+c的顶点坐标为（1，﹣3），则抛物线对应的函数解析式为（　　）

A、y=x²﹣2x+2 B、y=x²﹣2x﹣2 C、y=﹣x²﹣2x+1 D、y=x²﹣2x+1

查看试题解析
9. 如图，往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水，水面高度为6cm，现将右边细管绕A处顺时针旋转60°到AB位置，且左边细管位置不变，则此时“U”形装置左边细管内水柱的高度约为（）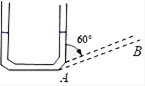

A、4cm B、2 $\sqrt{3}$ cm C、3cm D、8cm

查看试题解析
10. 二次函数y＝ax²+bx+c（a、b、c为常数，且a≠0）的图象如图所示，给出下列结论：①b²＞4ac； ②abc＜0；③a＜b； ④b+c＞3a；⑤方程ax²+bx+c＝0的两根之和的一半大于﹣1.其中，正确的结论有（）

A、①②③⑤ B、.①②④⑤ C、①②④ D、.①②③④⑤

查看试题解析

二、填空题

11. 已知一元二次方程有一个根是1，那么这个方程可以是.（写一个即可）

查看试题解析
12. 把抛物线y＝x²﹣2x+5的图象向下平移2个单位，再向左移动1个单位，得到的新图象的解析式为.

查看试题解析
13. 实验中学举行中国古诗词大赛，四道题分别是①锄禾日当午； ②春眠不觉晓；③白日依山尽；④床前明月光.要求甲乙两选手任选一道题在自己的答题板上写出下一句，他们选取的诗句恰好相同的概率是.

查看试题解析
14. 数学课上，老师让学生用尺规作图画Rt△ABC，使其斜边AB＝c，一条直角边BC＝a.小明的作法如图所示，你认为小明这种作法中判断∠ACB是直角的依据是.

查看试题解析
15. 已知一块圆心角为300°的扇形铁皮，用它做一个圆锥形的烟囱帽（接缝忽略不计），若圆锥的底面圆的直径是80cm，则这块扇形铁皮的半径是cm.

查看试题解析
16. 如图，一段抛物线：y＝﹣x（x﹣2）（0≤x≤2）记为C₁ ，它与x轴交于点O，A₁；将C₁绕点A₁旋转180°得C₂ ，交x轴于点A₂；将C₂绕点A₂旋转180°得C₃ ，交x轴于点A3…如此进行下去，则C₂₀₁₉的顶点坐标是.

查看试题解析
17. 在平面直角坐标系xOy中，函数y＝ $\frac{k}{x}$ （x＞0）的图象G经过点A（4，1），直线l：y＝ $\frac{1}{4}$ x+b与图象G交于点B，与y轴交于点C.我们把横、纵坐标都是整数的点叫做整数点，记图象G在点A，B之间的部分与线段OA，OC，BC围成的区域（不含边界）为W，若b＝﹣2，则区域W内的整数点的个数为；

查看试题解析
18. 如图，矩形OABC的边OA，OC分别在x轴，y轴上，点B在第一象限，点D在边BC上，且∠AOD＝30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，点B′和B分别对应）.若AB＝2，反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象恰好经过A′，B，则k的值为.

查看试题解析

三、解答题

19. 解方程：

(1)、3x²﹣7x+4＝0

(2)、x²+2 $\sqrt{5}$ x﹣10＝0

查看试题解析
20. 体育课上，小明、小强、小华三人在足球场上练习足球传球，足球从一个人传到另一个人记为踢一次.如果从小强开始踢，经过两次踢球后，足球踢到小华处的概率是多少？经过三次踢球后，足球踢回到小强处的概率呢？（列表或画树形图或列举）

查看试题解析
21. 如图，AB是⊙O的直径，半径OC⊥AB，过OC的中点D作弦EF∥AB.

(1)、求∠ABE的度数；

(2)、若DE＝2 $\sqrt{3}$ ，求⊙O的半径.

查看试题解析
22. 阅读理解：
如图（1），在平面直角坐标系xOy中，已知点A的坐标是（1，2），点B的坐标是（3，4），过点A、点B作平行于x轴、y轴的直线相交于点C，得到Rt△ABC，由勾股定理可得，线段AB＝ $\sqrt{A C^{2} + B C^{2}} = \sqrt{{(3 - 1)}^{2} + {(4 - 2)}^{2}} = 2 \sqrt{2}$ .

得出结论：

(1)、若A点的坐标为（x₁ ， y₁），B点的坐标为（x₂ ， y₂）请你直接用A、B两点的坐标表示A、B两点间的距离；
应用结论：

(2)、若点P在y轴上运动，试求当PA＝PB时，点P的坐标.

(3)、如图（2）若双曲线L₁：y＝ $\frac{k}{x}$ （x＞0）经过A（1，2）点，将线段OA绕点O旋转，使点A恰好落在双曲线L₂：y＝﹣ $\frac{k}{x}$ （x＞0）上的点D处，试求A、D两点间的距离.

查看试题解析
23. 已知一元二次方程x²+（2m+1）x+m²﹣1＝0.

(1)、若方程有两个不相等的实数根，试求m的取值范围；

(2)、若抛物线y＝x²+（2m+1）x+m²﹣1与直线y＝x+m没有交点，试求m的取值范围；

(3)、求证：不论m取何值，抛物线y＝x²+（2m+1）x+m²﹣1图象的顶点都在一条定直线上.

查看试题解析
24. 某市实施产业精准扶贫，帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克，到了收获季节投入市场销售时，调查市场行情后，发现该蜜柚不会亏本，且每天的销售量y（千克）与销售单价x（元）之间的函数关系如图所示.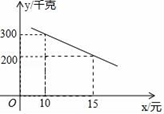

(1)、求y与x的函数关系式，并写出x的取值范围；

(2)、当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

(3)、某村农户今年共采摘蜜柚12000千克，若该品种蜜柚的保质期为50天，按照（2）的销售方式，能否在保质期内全部销售完这批蜜柚？若能，请说明理由；若不能，应定销售价为多少元时，既能销售完又能获得最大利润？

查看试题解析
25. 如图，抛物线L：y＝﹣x²+bx+c经过坐标原点，与它的对称轴直线x＝2交于A点.

(1)、直接写出抛物线的解析式；

(2)、⊙A与x轴相切，交y轴于B、C点，交抛物线L的对称轴于D点，恒过定点的直线y＝kx﹣2k+8（k＜0）与抛物线L交于M、N点，△AMN的面积等于2，试求：
①弧BC的长；

②k的值.

查看试题解析