湖北省黄石市协作体2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-03 类型:期末考试
一、单选题
-
1. 给出下列一组数: , , , , ,其中无理数的个数为( )A、0 B、1 C、2 D、32. 下列四个图形中,既是轴对称图形又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个3. 学生作业本每页大约为7.5忽米(1厘米=1000忽米),请用科学记数法将7.5忽米记为米,则正确的记法为( )A、7.5× 米 B、0.75× 米 C、0.75× 米 D、7.5× 米4. 下列运算中,正确的是( ).A、 B、 C、 D、5. 对于非零实数 ,规定 ,若 ,则 的值为( )A、 B、 C、 D、6. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )
A、4个 B、3个 C、2个 D、1个3. 学生作业本每页大约为7.5忽米(1厘米=1000忽米),请用科学记数法将7.5忽米记为米,则正确的记法为( )A、7.5× 米 B、0.75× 米 C、0.75× 米 D、7.5× 米4. 下列运算中,正确的是( ).A、 B、 C、 D、5. 对于非零实数 ,规定 ,若 ,则 的值为( )A、 B、 C、 D、6. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )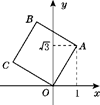 A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)7. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)7. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )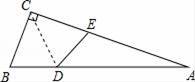 A、44° B、60° C、67° D、77°8. 如图,A,B,C三点在⊙O上,且∠AOB=80°,则∠ACB等于( )
A、44° B、60° C、67° D、77°8. 如图,A,B,C三点在⊙O上,且∠AOB=80°,则∠ACB等于( ) A、100° B、80° C、50° D、40°9. 如图,正比例函数y=x与反比例函数 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于 的函数值时,x的取值范围是( )
A、100° B、80° C、50° D、40°9. 如图,正比例函数y=x与反比例函数 的图象交于A(2,2)、B(﹣2,﹣2)两点,当y=x的函数值大于 的函数值时,x的取值范围是( ) A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>210. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
A、x>2 B、x<﹣2 C、﹣2<x<0或0<x<2 D、﹣2<x<0或x>210. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )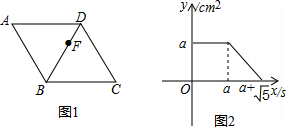 A、 B、2 C、 D、2
A、 B、2 C、 D、2二、填空题
-
11. 使二次根式 有意义的x的取值范围是.12. 分解因式: =.13. 分式方程 的解为.14. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC=25°.求∠P的度数.
 15. 桌上放有完全相同的三张卡片,卡片上分别标有数字2,1,4,随机摸出一张卡片(不放回),其数字为p,随机摸出另一张卡片,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是.16. 如图,在平面直角坐标系中,函数 和 的图象分别为直线 , ,过点(1,0)作 轴的垂线交 于点 ,过 点作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,…依次进行下去,则点 的坐标为.
15. 桌上放有完全相同的三张卡片,卡片上分别标有数字2,1,4,随机摸出一张卡片(不放回),其数字为p,随机摸出另一张卡片,其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是.16. 如图,在平面直角坐标系中,函数 和 的图象分别为直线 , ,过点(1,0)作 轴的垂线交 于点 ,过 点作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,…依次进行下去,则点 的坐标为.
三、解答题
-
17. 计算:| -2|+2﹣1﹣cos60°﹣(1﹣ )0.18. 先化简,再求值: · ,其中 满足19. 解不等式组 ,将解集在数轴上表示出来,并求出此不等式组的所有整数解.20. 关于x的一元二次方程为(m-1)x2-2mx+m+1=0(1)、求出方程的根;(2)、m为何整数时,此方程的两个根都为正整数?21. 为了解决农民工子女就近入学问题,我市某小学计划2019年秋季学期扩大办学规模,学校决定开支80000元全部用于购买课桌凳、办公桌椅和电脑,要求购买的课桌凳与办公桌椅的数量比为20:1,购买电脑的资金不低于16000 元,但不超过24000元.已知一套办公桌椅比一套课桌凳贵80元,用2000 元恰好可以买到10套课桌凳和4套办公桌椅(课桌凳和办公桌椅均成套购进).(1)、一套课桌凳和一套办公桌椅的价格分别为多少元?(2)、求出课桌凳和办公桌椅的购买方案.22. 如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连结AC,将△ACE沿AC翻转得到△ACF,直线FC与直线AB相交于点G.
 (1)、求证:FG是⊙O的切线;(2)、若B为OG的中点,CE= ,求⊙O的半径长;(3)、①求证:∠CAG=∠BCG;
(1)、求证:FG是⊙O的切线;(2)、若B为OG的中点,CE= ,求⊙O的半径长;(3)、①求证:∠CAG=∠BCG;②若⊙O的面积为4π,GC=2 ,求GB的长.
23. 如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C. (1)、求抛物线的解析式;(2)、若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)、P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)、P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.