河南省驻马店市新蔡县2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-03 类型:期末考试
一、单选题
-
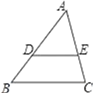
1. 已知函数y= 在实数范围内有意义,则自变量x的取值范围是( )A、x≥2 B、x>3 C、x≥2且x≠3 D、x>22. 若关于x的一元二次方程2x2﹣3x﹣k=0的一个根为1,则另一个根为( )A、2 B、﹣1 C、 D、3. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为( )
 A、2 B、4 C、6 D、84. 下列各式计算正确的是( )A、 + = B、4 -3 =1 C、2 ×3 =6 D、 ÷ =35. 小明和小亮在玩“石头、剪子、布”的游戏,两人一起做同样手势的概率是( )A、 B、 C、 D、6. 若关于x的方程x2﹣ x+sina=0有两个相等的实数根,则锐角a为( )A、75° B、60° C、45° D、30°7. 如图,E为平行四边形ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则平行四边形ABCD的面积为( )
A、2 B、4 C、6 D、84. 下列各式计算正确的是( )A、 + = B、4 -3 =1 C、2 ×3 =6 D、 ÷ =35. 小明和小亮在玩“石头、剪子、布”的游戏,两人一起做同样手势的概率是( )A、 B、 C、 D、6. 若关于x的方程x2﹣ x+sina=0有两个相等的实数根,则锐角a为( )A、75° B、60° C、45° D、30°7. 如图,E为平行四边形ABCD的边AB延长线上的一点,且BE:AB=2:3,△BEF的面积为4,则平行四边形ABCD的面积为( ) A、30 B、27 C、14 D、328. 如图,各正方形的边长均为1,则四个阴影三角形中,一定相似的一对是( )
A、30 B、27 C、14 D、328. 如图,各正方形的边长均为1,则四个阴影三角形中,一定相似的一对是( ) A、①② B、①③ C、②③ D、②④9. 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A、①② B、①③ C、②③ D、②④9. 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( ) A、( ,﹣1) B、(1,﹣ ) C、( ,﹣ ) D、(﹣ , )10. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作 EF∥AD,与AC,DC 分别交于点G,F,H为CG的中点,连结DE, EH,DH,FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若 ,则 .其中结论正确的有( )
A、( ,﹣1) B、(1,﹣ ) C、( ,﹣ ) D、(﹣ , )10. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作 EF∥AD,与AC,DC 分别交于点G,F,H为CG的中点,连结DE, EH,DH,FH.下列结论:①EG=DF;②△EHF≌△DHC;③∠AEH+∠ADH=180°;④若 ,则 .其中结论正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 将根式 , , , 化成最简二次根式后,随机抽取其中一个根式,能与 的被开方数相同的概率是.12. 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.如果x=-1是方程的根,则△ABC是三角形.13. 如图,在△ABC中,点D,点E分别是AB,AC的中点,点F是DE上一点,∠AFC=90°,BC=10cm,AC=6cm,则DF=cm.
 14. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的
14. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5 m,CD=8 m,则树高AB=
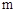 .
. 15. 两年前生产1t药品的成本是6000元,现在生产1t药品的成本是4860元,则药品成本的年平均下降率是.
15. 两年前生产1t药品的成本是6000元,现在生产1t药品的成本是4860元,则药品成本的年平均下降率是.三、解答题
-
16.(1)、解方程:(x+3)2=(1﹣3x)2.(2)、计算:(2﹣ )2+ +2sin30°tan60°.17. 已知关于x的方程 .(1)、若该方程的一个根为2,求a的值及该方程的另一根.(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.18. 如图,小明在教学楼的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为10米.请你帮助小明计算树的高度(精确到0.1米).
 19. 如图,在边长均为 的小正方形网格纸中, 的顶点 、 、 均在格点上, 为直角坐标系的原点,点 在 轴上.
19. 如图,在边长均为 的小正方形网格纸中, 的顶点 、 、 均在格点上, 为直角坐标系的原点,点 在 轴上. (1)、以 为位似中心,将 放大,使得放大后的 与 的相似比为 ,要求所画 与 在原点两侧;(2)、分别写出 、 的坐标.20. 如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
(1)、以 为位似中心,将 放大,使得放大后的 与 的相似比为 ,要求所画 与 在原点两侧;(2)、分别写出 、 的坐标.20. 如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似? 21. 石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.(1)、设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)(2)、每件童装降价多少元时,平均每天赢利1200元.(3)、要想平均每天赢利2000元,可能吗?请说明理由.22. 如图,AC是▱ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
21. 石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.(1)、设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)(2)、每件童装降价多少元时,平均每天赢利1200元.(3)、要想平均每天赢利2000元,可能吗?请说明理由.22. 如图,AC是▱ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G. (1)、若∠ABF=∠ACF,求证:CE2=EF•EG;(2)、若DG=DC,BE=6,求EF的长.23. 如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c= +8.
(1)、若∠ABF=∠ACF,求证:CE2=EF•EG;(2)、若DG=DC,BE=6,求EF的长.23. 如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c= +8. (1)、求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;(2)、直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;(3)、点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求 的值.
(1)、求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;(2)、直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;(3)、点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求 的值.