河南省周口市川汇区2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-03 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} = x$ 的实数根是（）

A、0或1 B、0 C、1 D、±1

查看试题解析
2. 令函数 $f (x) = - x^{2} + 2 x + m$ （m是常数），当 $x$ 取 $- 1$ ，1，2时，对应的函数值 $f (- 1)$ ， $f (1)$ ， $f (2)$ 大小关系是（）

A、 $f (- 1)$ ＜ $f (1)$ ＜ $f (2)$ B、 $f (- 1)$ ＜ $f (2)$ ＜ $f (1)$ C、 $f (2)$ ＜ $f (1)$ ＜ $f (- 1)$ D、 $f (1)$ ＜ $f (2)$ ＜ $f (- 1)$

查看试题解析
3. 在平面直角坐标系内，线段MN的两个端点坐标分别为M（-1，2）、N（2，1），平移线段MN得到线段M′N′，若M′的坐标为（0，1），则N′的坐标为（）

A、（3，0） B、（1，2） C、（1，0） D、（3，2）

查看试题解析
4. 下列事件中，是必然事件的是（）

A、任意掷一枚骰子一定出现奇数点 B、彩票中奖率20%，买5张一定中奖 C、晚间天气预报说明天有小到中雪 D、在13同学中至少有2人生肖相同

查看试题解析
5. 如图，已知点 $A (4 ， 0)$ ， $B (0 ， 3)$ ，点P在线段AB上（不与端点重合），反比例函数 $y = \frac{k}{x}$ 的图象经过点P，则 $k$ 的取值范围是（）

A、 $k$ ＞3 B、0≤ $k$ ≤3 C、0＜ $k$ ≤3 D、 $k$ ≥3

查看试题解析
6. 在直角坐标系中，已知点 $A (6 ， - 3)$ ，以原点O为位似中心，相似比为 $\frac{1}{3}$ ，把线段OA缩小为 $O A'$ ，则点A的坐标为（）

A、 $(2 ， - 1)$ ， $(- 2 ， - 1)$ B、 $(- 2 ， 1)$ ， $(2 ， 1)$ C、 $(2 ， 1)$ ， $(- 2 ， - 1)$ D、 $(2 ， - 1)$ ， $(- 2 ， 1)$

查看试题解析
7. 如图，△ABC的顶点是正方形网格的格点，则 $\cos A =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
8. 如图，在正方形ABCD中，边长为1，点E是BC边上的动点，过点E作AE的垂线交CD边于点F，设 $B E = x$ ， $F D = y$ ， $y$ 关于 $x$ 的函数关系图象如图所示，则 $m =$ （）

A、 $1.5$ B、2 C、2.5 D、3

查看试题解析
9. 方程有无实数解，可以通过构造函数，利用函数图象有无交点来判断.一元三次方程 $x^{3} + 2 x + 1 = 0$ 的实数解的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

10. $\sin 30 ° \cdot \cos 45 ° \cdot \tan 60 ° =$ .

查看试题解析
11. 在平面直角坐标系中，把抛物线 $y = - 3 x^{2}$ 向下平移2个单位长度，再向左平移1个单位长度，得到的新抛物线解析式为.

查看试题解析
12. 已知点 $A (1 ， a)$ ， $B (2 ， b)$ 在反比例函数 $y = - \frac{2}{x}$ 的图象上，则 $a$ ， $b$ 的大小关系是.

查看试题解析
13. 在一次摸球实验中，摸球箱内放有白色、黄色乒乓球共50个，这两种乒乓球的大小、材质都相同.小明发现，摸到白色乒乓球的频率稳定在60%左右，则箱内黄色乒乓球的个数很可能是.

查看试题解析
14. 如图， $∠ M O N = 90 °$ ，点A，B分别在射线OM，ON上， $A B = 4$ ，点C是线段AB的中点，△A'OC与△AOC关于直线OC对称.A'O与AB相交于点D.当△A'DC是直角三角形时，△OAB的面积等于.

查看试题解析

三、解答题

15. 已知关于 $x$ 的方程 $3 x^{2} - 6 x + 3 p = 0$ ，其中 $p$ 是常数.请用配方法解这个一元二次方程.

查看试题解析
16. 某商品投放市场试售：以每件65元销售时，每星期可卖出250件；以每件70元销售时，每星期可卖出200件.设每件售价x（元），销售量为y（件），销售总利润为w（元）.

(1)、若销售量与商品价格存在一次函数关系，请求出它们的关系式；

(2)、在⑴的函数关系下，若商品的进价为每件40元，如何定价才能使利润最大？

查看试题解析
17. 有4张看上去无差别的卡片，上面分别写着1，2，3，4.小华随机抽取1张，记下数字为x，小芳在剩余的3张卡片中随机取出1张，记下数字为y，这样确定了点M的坐标 $(x ， y)$ .

(1)、画出树状图或列表，写出点M所有可能的坐标；

(2)、求点M在函数 $y = x - 1$ 的图象上的概率.

查看试题解析
18. 在一次“数学实践”活动中，小明沿一条南北公路向北行走，在A处，他测得左边建筑物C在北偏西30°方向，右边建筑物D在北偏东30°方向；从A处向北40米行至B处，他又测得左边建筑物C在北偏西60°方向，右边建筑物D在北偏东45°方向.请根据以上数据求两建筑物C、D到这条南北公路的距离.（参考数据： $\sqrt{3} \approx 1.732$ ， $\sqrt{2} \approx 1.414$ .结果精确到0.1米）

查看试题解析
19. 如图， $P A ⊥ x$ 轴于点A，连接 $O P$ ， $P A$ ， $P O$ 分别与反比例函数 $y = \frac{k}{x}$ （ $k$ ＞0）的图象交于点B，C.

(1)、求证： $\frac{A B}{A P} = \frac{O C^{2}}{O P^{2}}$ ；

(2)、已知 $P (4 ， 3)$ ， $P B = P C$ ，求 $k$ 的值.

查看试题解析
20. 如图，点I是△ABC的内心，AI的延长线交BC于点D，与△ABC的外接圆相交于点E，连接BE.

(1)、求证： $B E = I E$ ；

(2)、若 $A D = 6$ ， $D E = 2$ ，求 $A I$ 的长.

查看试题解析
21. 如图

(1)、问题发现
如图1，△ABC和△CDE均为等边三角形，直线AD和直线BE交于点F.

填空：① $∠ A F B$ 的度数是；②线段AD，BE之间的数量关系为；

(2)、类比探究
如图2，△ABC和△CDE均为等腰直角三角形， $∠ A B C = ∠ D E C = 90 °$ ， $A B = B C$ ， $D E = E C$ ，直线AD和直线BE交于点F.请判断 $∠ A F B$ 的度数及线段AD，BE之间的数量关系，并说明理由.

(3)、解决问题
如图3，在△ABC中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $A B = 5$ ，点D在AB边上， $D E ⊥ A C$ 于点E， $A E = 3$ ，将△ADE绕着点A在平面内旋转，请直接写出直线DE经过点B时，点C到直线DE的距离.

查看试题解析
22. 如图，在平面直角坐标系中，直线y＝kx﹣4k+4与抛物线y＝ $\frac{1}{4}$ x²﹣x交于A、B两点.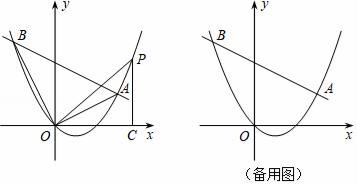

(1)、直线总经过定点，请直接写出该定点的坐标；

(2)、点P在抛物线上，当k＝﹣ $\frac{1}{2}$ 时，解决下列问题：
①在直线AB下方的抛物线上求点P，使得△PAB的面积等于20；

②连接OA，OB，OP，作PC⊥x轴于点C，若△POC和△ABO相似，请直接写出点P的坐标.

查看试题解析