河南省郑州市上街区2019届九年级上学期数学期末考试试卷（中考一模）
试卷更新日期：2020-01-03 类型：期末考试
一、单选题
-
1. 在 ， ，﹣2，﹣1中，最小的数是（ ）A、 B、 C、﹣2 D、﹣12. 2018年10月24日港珠澳大桥全线通车，港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连接珠海和澳门人工岛，止于珠海洪湾，它是世界上最长的跨海大桥，被称为“新世界七大奇迹之一”，港珠澳大桥总长度55000米，则数据55000用科学记数法表示为（ ）A、55×105 B、5.5×104 C、0.55×105 D、5.5×1053. 如图，是由几个大小相同的小立方块所搭几何体的俯视图，其中小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的主视图是（ ）
A、
B、
C、
D、
4. 已知点M（1﹣2m，1﹣m）关于x轴的对称点在第四象限，则m的取值范围在数轴上表示正确的是（ ）A、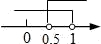
B、
C、
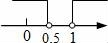D、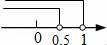
5. 如图，在△ABC中，BA＝BC，∠ABC＝120°，AB的垂直平分线交AC于点M，交AB于点E，BC的垂直平分线交AC于点N，交BC于点F，连接BM，BN，若AC＝24，则△BMN的周长是（ ）
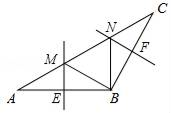A、36 B、24 C、18 D、166. 用A，B两个机器人搬运化工原料，A机器人比B机器人每小时多搬运30kg，A机器人搬运900kg所用时间与B机器人搬运600kg所用时间相等，设A机器人每小时搬运xkg化工原料，那么可列方程（ ）A、 ＝ B、 ＝ C、 ＝ D、 ＝7. 如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是（ ）
A、 B、 C、 D、8. 小明从家出发到公园晨练，在公园锻炼一段时间后按原路返回，同时小明爸爸从公园按小明的路线返回家中，如图是两人离家的距离y（米）与小明出发的时间x（分）之间的函数图象，则下列结论中不正确的是（ ）
A、公园离小明家1600米 B、小明出发 分钟后与爸爸第一次相遇 C、小明在公园停留的时间为5分钟 D、小明与爸爸第二次相遇时，离家的距离是960米9. 远古时期，人们通过在绳子上打结来的记录数量，即“结绳计数”，如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（ ）
A、336 B、510 C、1326 D、360310. 如图，已知AM为△ABC的角平分线，MN∥AB交AC于点N，如果AN：NC=2：3，那么AC：AB等于（ ）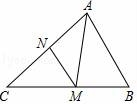
A、3：1 B、3：2 C、5：3 D、5：2二、填空题
-
11. 计算： =.12. 如图，六边形ABCDEF的六个角都是120°，边长AB＝1cm，BC＝3cm，CD＝3cm，DE＝2cm，则这个六边形的周长是：.
13. 已知关于x的方程（k﹣1）x2﹣2kx+k﹣3=0有两个相等的实根，则k的值是 ．14. 如图，△ABB1 ， △A1B1B2 ， …，△An﹣2Bn﹣2Bn﹣1 ， △An﹣1Bn﹣1Bn是n个全等的等腰三角形，其中AB=2，BB1=1，底边BB1 ， B1B2 ， …，Bn﹣2Bn﹣1 ， Bn﹣1Bn在同一条直线上，连接ABn交An﹣2Bn﹣1于点P，则PBn﹣1的值为.
15. 如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD的内部，将AF延长后交边BC于点G，且 ，则 的值为.
三、解答题
-
16. 先化简，再求值：（ - ）÷ - +x，其中x满足方程x2-5x+2=017. 某校对七年级300名学生进行了教学质量监测（满分100分），现从中随机抽取部分学生的成绩进行整理，并绘制成如图不完整的统计表和统计图：
注：60分以下为“不及格”，60～69分为“及格”，70～79分为“良好”，80分及以上为“优秀”
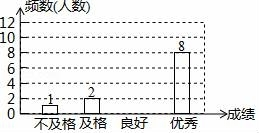
请根据以上信息回答下列问题：
(1)、补全统计表和统计图；(2)、若用扇形统计图表示统计结果，则“良好”所对应扇形的圆心角为多少度？(3)、请估计该校七年级本次监测成绩为70分及以上的学生共有多少人？18. 如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F。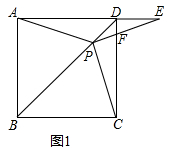
(1)、证明：PC=PE；(2)、求∠CPE的度数；(3)、如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系．并说明理由．
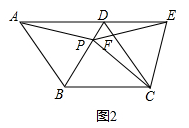19. 如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15m，CD=20m．AB和CD之间有一景观池，小双在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°，点B、E、D在同一直线上．求两幢建筑物之间的距离BD．（结果精确到0.1m）（参考数据：sin42°=0.67，cos42°=0.74，tan42°=0.90）
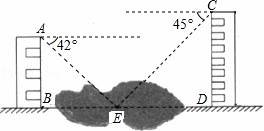20. 如图，一次函数 与反比例函数 的图象交于A（1，4），B（4，n）两点.
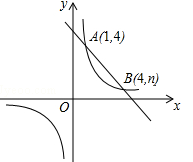(1)、求反比例函数的解析式；(2)、求一次函数的解析式；(3)、点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小.21. 如图，有长为24m的篱笆，现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB为xm，面积为Sm2.
(1)、求S与x的函数关系式及x值的取值范围；(2)、要围成面积为45m2的花圃，AB的长是多少米？(3)、当AB的长是多少米时，围成的花圃的面积最大？22. 如图，Rt△AOB在平面直角坐标系中，已知：B（0， ），点A在x轴的正半轴上，OA=3，∠BAD=30°，将△AOB沿AB翻折，点O到点C的位置，连接CB并延长交x轴于点D.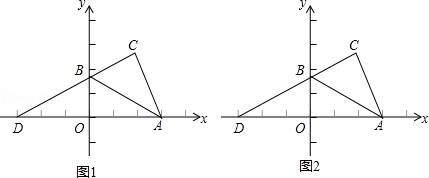
(1)、求点D的坐标；(2)、动点P从点D出发，以每秒2个单位的速度沿x轴的正方向运动，当△PAB为直角三角形时，求t的值；(3)、在（2）的条件下，当△PAB为以∠PBA为直角的直角三角形时，在y轴上是否存在一点Q使△PBQ为等腰三角形？如果存在，请直接写出Q点的坐标；如果不存在，请说明理由.23. 在平面直角坐标系中，抛物线 与 轴的两个交点分别为A（-3，0）、B（1，0），与y轴交于点D(0，3)，过顶点C作CH⊥x轴于点H.
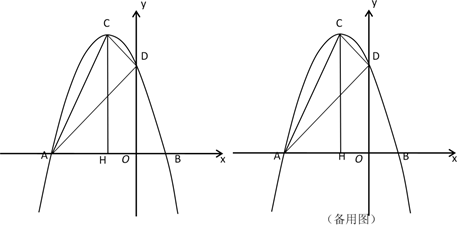(1)、求抛物线的解析式和顶点C的坐标；(2)、连结AD、CD，若点E为抛物线上一动点（点E与顶点C不重合），当△ADE与△ACD面积相等时，求点E的坐标；(3)、若点P为抛物线上一动点（点P与顶点C不重合），过点P向CD所在的直线作垂线，垂足为点Q，以P、C、Q为顶点的三角形与△ACH相似时，求点P的坐标.