河南省许昌市2019届九年级上学期数学期末考试试卷
试卷更新日期：2020-01-03 类型：期末考试
一、单选题
-
1. 下列四个手机应用图标中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
2. 点P（3，5）关于原点对称的点的坐标是（ ）A、（﹣3，5） B、（3，﹣5） C、（5，3） D、（﹣3，﹣5）3. 若方程x2-2x+m=0有两个相等实数根，则m=（ ）A、-2 B、0 C、1 D、4. 两圆的半径分别为2和5，圆心距为7，则这两圆的位置关系为（ ）A、外离. B、外切. C、相交. D、内切.5. 在Rt△ABC中，∠C=90°，AB=10，sinB= ，则BC的长是（ ）A、 B、4 C、 D、6. 如图，在⊙O中，∠ABC=50°，则∠AOC等于（ ）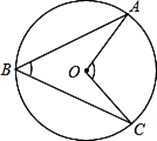
A、50° B、80° C、90° D、100°7. 若点(-2， )，(-1， )，(1， )在反比例函数 的图像上，则下列结论中，正确的是（ ）A、 > > B、 > > C、 > > D、 > >8. 在一幅长 ，宽 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整幅挂图的面积是 ，设金色纸边的宽为 ，那么 满足的方程是（ ）
A、 B、 C、 D、9. 如图，AB//CD，AD与BC相交于点O，若AO=2，DO=4，BO=3，则BC的长为（ ）
A、6 B、9 C、12 D、1510. 如图，已知△ABC的顶点坐标分别为A(0，2)，B(1，0)，C(2，1).若二次函数y=x2+bx+1的图像与阴影部分(含边界)一定有公共点，则实数b的取值范围是（ ）
A、b≤-2 B、b<-2 C、b≥-2 D、b>-2二、填空题
-
11. 方程4x2-4x+1=0的解为.12. 写出一个图象在第二、四象限的反比例函数解析式：.13. 如图是一个直径为10cm的圆柱形输油管的横截面，若油面宽AB=8cm，则油面的深度为.
14. 如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF长为10cm，母线OE（OF）长为10cm.在母线OF上的点A处有一块爆米花残渣，且FA=2cm，一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点，则此蚂蚁爬行的最短距离cm.
15. 在△ABC中，∠ACB=90°，AC=BC，P是△ABC内一点，且满足PA=3，PB=1，PC=2，则∠BPC的度数为.三、解答题
-
16. 如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，其中点A（5，4），B（1，3），将△AOB绕点O逆时针旋转90°后得到△A1OB1 ．
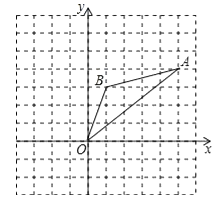(1)、画出△A1OB1；(2)、在旋转过程中点B所经过的路径长为；
(3)、求在旋转过程中线段AB、BO扫过的图形的面积之和．
17. 老师和小明同学玩数学游戏，老师取出一个不透明的口袋，口袋中装有三张分别标有数字1，2，3的卡片，卡片除数字个其余都相同，老师要求小明同学两次随机抽取一张卡片，并计算两次抽到卡片上的数字之积是奇数的概率，于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果，题20图是小明同学所画的正确树状图的一部分.(1)、补全小明同学所画的树状图；(2)、求小明同学两次抽到卡片上的数字之积是奇数的概率.18. 阅读下面的材料：∵ax2+bx+c=0(a≠0)的根为 ，
∴ ， ；请利用这一结论解决下列问题：
(1)、若ax2+bx+c=0的两根为－2和3，求b和c的值.(2)、设方程2x2-3x+1=0的两根为x1、x2 ， 不解方程，求 的值.19. 某游乐场部分平面图如图所示，C，E，A在同一直线上，D、E、B在同一直线上，∠BAE=30°，∠C=90°，∠ABE=90°，测得A处与C处的距离为100米，B处与D处的距离为80米，求海洋球D处到过山车C处的距离.(结果精确到0.1米)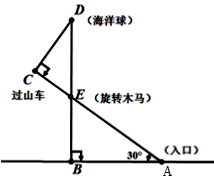
20. 为进一步促进义务教育均衡发展，某市加大了基础教育经费的投入，已知2015年该市投入基础教育经费5000万元，2017年投入基础教育经费7200万元．(1)、求该市这两年投入基础教育经费的年平均增长率；(2)、如果按(1)中基础教育经费投入的年平均增长率计算，该市计划2018年用不超过当年基础教育经费的5%购买电脑和实物投影仪共1500台，调配给农村学校．若购买一台电脑需3500元，购买一台实物投影需2000元，则最多可购买电脑多少台？21. 如图，在平面直角坐标系中，一次函数y1=kx+b的图象分别交x轴，y轴于A、B两点，与反比例函数y2= 的图象交于C、D两点，已知点C的坐标为（﹣4，﹣1），点D的横坐标为2．
(1)、求反比例函数与一次函数的解析式；(2)、直接写出当x为何值时，y1＞y2？
(3)、点P是反比例函数在第一象限的图象上的点，且点P的横坐标大于2，过点P做x轴的垂线，垂足为点E，当△APE的面积为3时，求点P的坐标．
22. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E.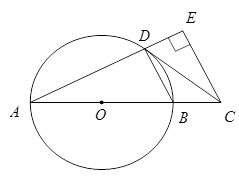
(1)、求证：∠BDC=∠A；(2)、若CE=4，DE=2，求AD的长.23. 如图1，在平面直角坐标系中，已知抛物线y=ax2+bx-5与x轴交于A(-1，0)，B(5，0)两点，与y轴交与点C.
(1)、求抛物线的函数表达式；(2)、若点D是y轴上的点，且以B、C、D为顶点的三角形与△ABC相似，求点D的坐标；(3)、如图2，CE//x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别相交于点F，G，试探求当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积.