河南省南阳市淅川县2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-03 类型:期末考试
一、单选题
-
1. 方程(x+1)(x﹣3)=0的根是( )A、x=﹣1 B、x=3 C、x1=1,x2=3 D、x1=﹣1,x2=32. 计算 + 的值等于( )A、 B、4 C、5 D、2 +23. 如图,已知:直线a∥b,AP:PB=3:2,CD=n,则线段CP的值等于( )
 A、 B、 C、 D、4. 已知关于y的方程y2-3y=a没有实数根,则a的取值范围是( )A、 B、 C、 D、5. 在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )A、 B、 C、 或 D、 或6. 下列说法正确的是( )A、投掷三枚硬币正好三个都正面朝上是不可能事件 B、打开电视正在播新闻联播是随机事件 C、随机投掷一枚硬币正面朝上的概率是 ,是指将一枚硬币随机投掷10次,一定有5次正面朝上 D、确定事件的发生概率大于0而小于17. 如图,已知 与 位似,且 与 的周长之比为1:2,点 的坐标为 ,则点 的坐标为( )
A、 B、 C、 D、4. 已知关于y的方程y2-3y=a没有实数根,则a的取值范围是( )A、 B、 C、 D、5. 在Rt△ABC中,AC=8,BC=6,则cosA的值等于( )A、 B、 C、 或 D、 或6. 下列说法正确的是( )A、投掷三枚硬币正好三个都正面朝上是不可能事件 B、打开电视正在播新闻联播是随机事件 C、随机投掷一枚硬币正面朝上的概率是 ,是指将一枚硬币随机投掷10次,一定有5次正面朝上 D、确定事件的发生概率大于0而小于17. 如图,已知 与 位似,且 与 的周长之比为1:2,点 的坐标为 ,则点 的坐标为( )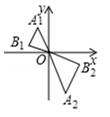 A、 B、 C、 D、8. 如图,已知:点A,B,C,D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
A、 B、 C、 D、8. 如图,已知:点A,B,C,D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( ) A、2 B、3 C、4 D、59. 如图是二次函数y=ax2+bx+c的图象,则下列结论错误的是( )
A、2 B、3 C、4 D、59. 如图是二次函数y=ax2+bx+c的图象,则下列结论错误的是( ) A、 B、 C、 D、10. 如图,⊙O的半径为1,动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示位置,第2秒B点P位于点C的位置,……,则第2017秒点P所在位置的坐标为( )
A、 B、 C、 D、10. 如图,⊙O的半径为1,动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示位置,第2秒B点P位于点C的位置,……,则第2017秒点P所在位置的坐标为( )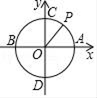 A、( , ) B、(- , ) C、(0,﹣1) D、( ,- )
A、( , ) B、(- , ) C、(0,﹣1) D、( ,- )二、填空题
-
11. 二次根式 有意义的条件是.12. 九(1)班为了选拔两名学生参加学校举行的“核心价值观知识竞赛”活动,在班级内先举行了预选赛,在预选赛中有两女、一男3位学生获得了一等奖,从获得一等奖的3位学生中随机抽取2名学生参加学校的比赛,则选出的2名学生恰好为一男一女的概率为.13. 如图是水平放置的水管截面示意图,已知水管的半径为50cm,水面宽AB=80cm,则水深CD约为cm.
 14. 如图,在Rt△ABC,∠C=90°,∠A=30°,BC=1,以顶点A、B为圆心,以AC、BC的长为半径的圆弧分别交AB于点D、E,则图中阴影部分的面积为.
14. 如图,在Rt△ABC,∠C=90°,∠A=30°,BC=1,以顶点A、B为圆心,以AC、BC的长为半径的圆弧分别交AB于点D、E,则图中阴影部分的面积为. 15. 如图,点E是矩形纸片的边BC上的一动点,沿直线AE折叠纸片,点B落在了点B′位置,连结CB′.已知AB=3,BC=6,则当线段CB′最小时BE的长为.
15. 如图,点E是矩形纸片的边BC上的一动点,沿直线AE折叠纸片,点B落在了点B′位置,连结CB′.已知AB=3,BC=6,则当线段CB′最小时BE的长为.
三、解答题
-
16. 计算:(3 )2-(2 +1)(2 -1)+3 (cos30°)-1-2017017. 已知二次函数y=- .
 (1)、将y=- +x+ 用配方法化为y=a(x-h)2+k的形式;(2)、求该函数图象与两坐标轴交点的坐标;(3)、画出该函数的图象.18. 如图,在建筑物M的顶端C处测得大楼N顶端B点的仰角α=45°,同时测得大楼底端A点的俯角为β=30°.已知建筑物M的高CD=20米,求楼高AB为多少米?( ≈1.732,结果精确到0.1米)
(1)、将y=- +x+ 用配方法化为y=a(x-h)2+k的形式;(2)、求该函数图象与两坐标轴交点的坐标;(3)、画出该函数的图象.18. 如图,在建筑物M的顶端C处测得大楼N顶端B点的仰角α=45°,同时测得大楼底端A点的俯角为β=30°.已知建筑物M的高CD=20米,求楼高AB为多少米?( ≈1.732,结果精确到0.1米) 19. 已知关于x的方程(m-1)x2-(m-2)x+ m=0.(1)、当m取何值时方程有一个实数根?(2)、当m取何值时方程有两个实数根?(3)、设方程的两根分别为x1、x2 , 且x1x2=m+1,求m的值.20. 某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.(1)、求y(元)关于x(元)的函数关系式,并写出x的取值范围.(2)、求当x取何值时y最大?并求出y的最大值.(3)、若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?21. 如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
19. 已知关于x的方程(m-1)x2-(m-2)x+ m=0.(1)、当m取何值时方程有一个实数根?(2)、当m取何值时方程有两个实数根?(3)、设方程的两根分别为x1、x2 , 且x1x2=m+1,求m的值.20. 某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.(1)、求y(元)关于x(元)的函数关系式,并写出x的取值范围.(2)、求当x取何值时y最大?并求出y的最大值.(3)、若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?21. 如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA. (1)、求证:CD是⊙O的切线.(2)、如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.22. 观察发现:如图(1),⊙O是△ADC的外接圆,点B是边CD上的一点,且△ABC是等边三角形.OD与AB交于点E,以O为圆心、OE为半径的圆交AB于点F,连接CF、OF.
(1)、求证:CD是⊙O的切线.(2)、如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.22. 观察发现:如图(1),⊙O是△ADC的外接圆,点B是边CD上的一点,且△ABC是等边三角形.OD与AB交于点E,以O为圆心、OE为半径的圆交AB于点F,连接CF、OF. (1)、求∠AOD的度数;(2)、线段AE、CF有何大小关系?证明你的猜想.
(1)、求∠AOD的度数;(2)、线段AE、CF有何大小关系?证明你的猜想.拓展应用:如图(2),△HJI是等边三角形,点K是IH延长线上的一点.点O是△JKI的外接圆圆心,OK与JH相交于点E.如果等边三角形△JHI的边长为2,请直接写出JE的最小值和此时∠JEO的度数.
23. 如图,已知抛物线y=-x2+bx+c与直线y=-x的交点A、B的横坐标分别为2和 .点P是直线上方抛物线上的一动点,过点P作PD⊥AB于点D,作PE⊥x轴交AB于点E. (1)、直接写出点A、B的坐标;(2)、求抛物线的关系式;(3)、判断△OBC形状,并说明理由;(4)、设点P的横坐标为n,线段PD的长为y,求y关于n的函数关系式;(5)、定义符号min{a,b)}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接写出min{-x2+bx+c,-x}的最大值.
(1)、直接写出点A、B的坐标;(2)、求抛物线的关系式;(3)、判断△OBC形状,并说明理由;(4)、设点P的横坐标为n,线段PD的长为y,求y关于n的函数关系式;(5)、定义符号min{a,b)}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接写出min{-x2+bx+c,-x}的最大值.