辽宁省锦州市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-03 类型:期末考试
一、单选题
-
1. 下列各实数为无理数的是( )A、 B、 C、﹣0.1 D、﹣2. 若 是关于x、y的方程x+ay=3的解,则a值为( )A、1 B、2 C、3 D、43. 在下列图形中,由条件∠1+∠2=180°不能得到AB∥CD的是( )A、
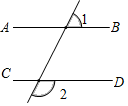 B、
B、 C、
C、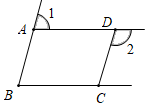 D、
D、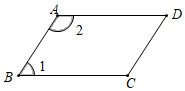 4. 为了了解阳光居民小区“全民健身”活动的开展情况,某志愿者随机调查了该小区50名成年居民一周的体育锻炼时间,并将数据进行整理后绘制成如图所示的统计图,则这50人一周体育锻炼时间的众数是( )
4. 为了了解阳光居民小区“全民健身”活动的开展情况,某志愿者随机调查了该小区50名成年居民一周的体育锻炼时间,并将数据进行整理后绘制成如图所示的统计图,则这50人一周体育锻炼时间的众数是( ) A、6小时 B、20人 C、10小时 D、3人5. 如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为( )
A、6小时 B、20人 C、10小时 D、3人5. 如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为( ) A、1 B、2 C、3 D、46. 均匀地向如图所示的容器中注满水,下列图象中,能反映在注水过程中水面高度h随时间t变化的函数关系的图象大致是( )
A、1 B、2 C、3 D、46. 均匀地向如图所示的容器中注满水,下列图象中,能反映在注水过程中水面高度h随时间t变化的函数关系的图象大致是( ) A、
A、 B、
B、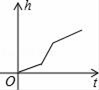 C、
C、 D、
D、 7. 如图,已知一次函数y=kx+2的图象与x轴,y轴分别交于点A,B,与正比例函数y= x交于点C,已知点C的横坐标为2,下列结论:①关于x的方程kx+2=0的解为x=3;②对于直线y=kx+2,当x<3时,y>0;③对于直线y=kx+2,当x>0时,y>2;④方程组 的解为 ,其中正确的是( )
7. 如图,已知一次函数y=kx+2的图象与x轴,y轴分别交于点A,B,与正比例函数y= x交于点C,已知点C的横坐标为2,下列结论:①关于x的方程kx+2=0的解为x=3;②对于直线y=kx+2,当x<3时,y>0;③对于直线y=kx+2,当x>0时,y>2;④方程组 的解为 ,其中正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
8. 实数8的立方根是 .9. 我校八年一班甲、乙两名同学10次投篮命中的平均数 均为7,方差 =1.45, =2.3,教练想从中选一名成绩较稳定的同学加入校篮球队,那么应选.10. 将直线y=2x+4沿y轴向下平移3个单位,则得到的新直线所对应的函数表达式为.11. 2018年6月14日,第21届世界杯足球赛在俄罗斯举行.小李在网上预定了小组赛和决赛两个阶段的门票共10张,总价为15800元,其中小组赛门票每张850元,决赛门票每张4500元,若设小李预定了小组赛门票x张,决赛门票y张,根据题意,可列方程组为.12. 对于函数y=(m﹣2)x+1,若y随x的增大而增大,则m的取值范围.13. 如图,∠A=80°,BO平分∠ABC,CO平分∠ACB,则∠BOC=°.
 14. 在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.右图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款元.
14. 在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.右图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款元. 15. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线 上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是.
15. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线 上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是.
三、解答题
-
16. 计算:(1)、 ﹣3 ﹣ ;(2)、( ﹣ )2•(5+2 )17. 用适当的方法解方程组:18. 随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
组別
家庭年文化教育消费金额x(元)
户数
A
x≤5000
36
B
5000<x≤10000
27
C
10000<x≤15000
m
D
15000<x≤20000
33
E
x>20000
30

请你根据统计图表提供的信息,解答下列问题:
(1)、本次被调查的家庭有户,表中m=;(2)、请说明本次调查数据的中位数落在哪一组?(3)、在扇形统计图中,D组所在扇形的圆心角为多少度?(4)、这个社区有2500户家庭,请你估计年文化教育消费在10000元以上的家庭有多少户?19. 如图,在平面直角坐标中,△ABC各顶点都在小方格的格点上.
①画出△ABC关于y轴对称的△A1B1C1 , 并写出△A1B1C1各顶点的坐标;
②在x轴上找一点P,使PA+PB1最短,画出图形并写出P点的坐标.
20. 已知,如图,AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.求证:AC⊥BD

请将下列证明过程中的空格补充完整.
证明:∵AB∥CD,
∴∠ABC=∠DCF.()
∵BD平分∠ABC,CE平分∠DCF,
∴∠2= ∠ABC,∠4= ∠DCF.()
∴.
∴BD∥CE.()
∴.(两直线平行,内错角相等)
∵∠ACE=90°,
∴∠BGC=90°,即AC⊥BD.()
21. 某校组织八年级师生共420人参观纪念馆,学校联系租车公司提供车辆,该公司现有A,B两种座位数不同的车型,如果租用A种车3辆,B种车5辆,则空余15个座位:如果租用A种车5辆,B种车3辆,则有15个人没座位(1)、求该公司A,B两种车型各有多少个座位?(2)、若A种车型的日租金为260元辆,B种车型的日租金为350元辆,怎样租车能使得座位恰好坐满且租金最少?最少租金是多少?(请直接写出答案)22. 某种水泥储存罐的容量为25m3 , 它有一个输入口和一个输出口.从某时刻开始,只打开输入口,匀速向储存罐内注入水泥,3min后,再打开输出口,匀速向运输车输出水泥,又经过2.5min水泥储存罐注满.已知水泥储存罐内的水泥量y(m3)与时间x(min)之间的函数图象如图所示. (1)、求每分钟向储存罐内注入的水泥量;(2)、当3≤x≤5.5时,求y与x之间的函数关系式;(3)、水泥储存罐每分钟向运输车输出的水泥量是多少立方米?23. 我们定义:
(1)、求每分钟向储存罐内注入的水泥量;(2)、当3≤x≤5.5时,求y与x之间的函数关系式;(3)、水泥储存罐每分钟向运输车输出的水泥量是多少立方米?23. 我们定义:在一个三角形中,如果一个角的度数是另一个角的度数 倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为 , , 的三角形是“和谐三角形”
概念理解:
如图, ,在射线 上找一点 ,过点 作 交 于点 ,以 为端点作射线 ,交线段 于点 (点 不与 重合)
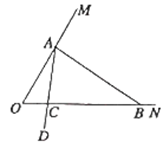 (1)、 的度数为 , (填“是”或“不是”)“和谐三角形”(2)、若 ,求证: 是“和谐三角形”.(3)、如图,点 在 的边 上,连接 ,作 的平分线 交于点 ,在 上取点 ,使 , .若 是“和谐三角形”,求 的度数.
(1)、 的度数为 , (填“是”或“不是”)“和谐三角形”(2)、若 ,求证: 是“和谐三角形”.(3)、如图,点 在 的边 上,连接 ,作 的平分线 交于点 ,在 上取点 ,使 , .若 是“和谐三角形”,求 的度数. 24. 如图,直线y= x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
24. 如图,直线y= x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称. (1)、求直线BC的函数表达式;(2)、设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
(1)、求直线BC的函数表达式;(2)、设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为 ,请直接写出点M的坐标.