辽宁省大连市中山区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-03 类型:期末考试
一、单选题
-
1. 下面四个手机应用图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若二次根式 有意义,则 的取值范围是( )A、x>3 B、 C、x<3 D、3. 若分式 的值为0,则x的值为A、3 B、 C、3或 D、04. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是( )
2. 若二次根式 有意义,则 的取值范围是( )A、x>3 B、 C、x<3 D、3. 若分式 的值为0,则x的值为A、3 B、 C、3或 D、04. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是( )
A、(4,1) B、(﹣1,4) C、(﹣4,﹣1) D、(﹣1,﹣4)5. 下列运算正确的是( )A、 B、 C、 D、6. 工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB 的边OA,OB 上分别取 OM=ON, 然后移动角尺使角尺的两边相同的刻度分别与 M,N 重合,得到∠AOB 的平分线 OP, 做法中用到三角形全等的判定方法是( )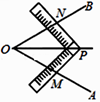 A、SSS B、SAS C、ASA D、AAS7. 下列计算 ﹣ 的结果是( )A、4 B、3 C、2 D、8. 如图,OC平分∠AOB,CM⊥OB于点M,CM=3,则点C到射线OA的距离为( )
A、SSS B、SAS C、ASA D、AAS7. 下列计算 ﹣ 的结果是( )A、4 B、3 C、2 D、8. 如图,OC平分∠AOB,CM⊥OB于点M,CM=3,则点C到射线OA的距离为( )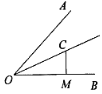 A、5 B、4 C、3 D、29. 计算 的结果为( )A、1 B、x C、 D、10. 运用乘法公式计算(x+3)2的结果是( )A、x2+9 B、x2–6x+9 C、x2+6x+9 D、x2+3x+9
A、5 B、4 C、3 D、29. 计算 的结果为( )A、1 B、x C、 D、10. 运用乘法公式计算(x+3)2的结果是( )A、x2+9 B、x2–6x+9 C、x2+6x+9 D、x2+3x+9二、填空题
-
11. 分解因式:3a2-3 .12.
如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为
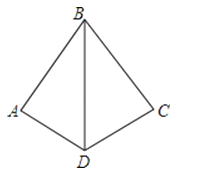 13. 计算: .14. 如图,已知线段AB,分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点F,在直线CD上任取一点E,连接EA、EB.若EA=5,则EB=.
13. 计算: .14. 如图,已知线段AB,分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点F,在直线CD上任取一点E,连接EA、EB.若EA=5,则EB=.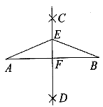 15. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD为∠CAB的角平分线,若CD=3,则DB=.
15. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD为∠CAB的角平分线,若CD=3,则DB=.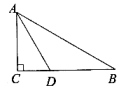
三、解答题
-
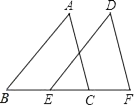
16. 计算:(1)、(2)、17. 计算:(1)、(2)、18. 如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
 19. 先化简再求值: 其中20. 甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?21. 【观察】方程 的解是 的解是 ;
19. 先化简再求值: 其中20. 甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?21. 【观察】方程 的解是 的解是 ;的解是 的解是
【发现】根据你的阅读回答问题:
(1)、 的解为;(2)、求关于 的方程 的解(用含 的代数式表示),并利用“方程的解的概念”验证.(3)、【类比】关于 的方程 的解为(用含 的代数式表示).22. 如图1,△ABC是等边三角形,点D是BC上一点,点E在CA的延长线上,连结EB、ED,且EB=ED.
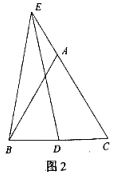 (1)、求证:∠DEC=∠ABE;(2)、点D关于直线EC的对称点为M,连接EM、BM:
(1)、求证:∠DEC=∠ABE;(2)、点D关于直线EC的对称点为M,连接EM、BM:①依题意将图2补全;
②求证:EB=BM.
23. 如图,某小区有一块长为 米、宽为 米的长方形地块该长方形地块。该长方形地块正中间是一个长为 米的长方形,四个角是大小相同的正方形,该小区计划将如图阴影部分进行绿化,对四个角的四个正方形采用A绿化方案,对正中间的长方形采用B绿化方案.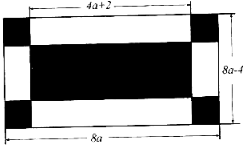 (1)、采用A绿化方案的每个正方形边长是多少米,采用B绿化方案的长方形另一边长是多少米(用含 的代数式表示);(2)、若采用A、B两种绿化方案的总造价相同,均为2700元,请你判断哪种方案单位面积造价高?并说明理由.24. 阅读下面材料:小明遇到这样一个问题:
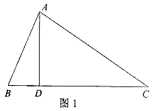
(1)、采用A绿化方案的每个正方形边长是多少米,采用B绿化方案的长方形另一边长是多少米(用含 的代数式表示);(2)、若采用A、B两种绿化方案的总造价相同,均为2700元,请你判断哪种方案单位面积造价高?并说明理由.24. 阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
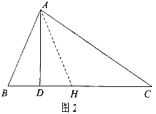
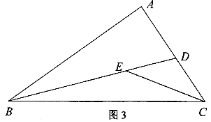 (1)、根据阅读材料,证明:BC=AB+2BD;(2)、参考小明的方法,解决下面的问题:
(1)、根据阅读材料,证明:BC=AB+2BD;(2)、参考小明的方法,解决下面的问题:如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。
25. 已知等腰Rt△ABC,∠BAC=90°,AB=AC,点D为△ABC内部一点,连接AD、BD、CD,点H为BD中点,连接AH,且∠BAH=∠ACD.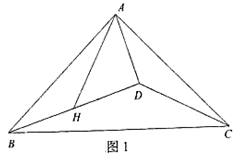
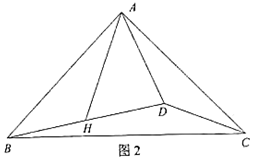 (1)、如图1,若∠ADB=90°,求证:∠DAH=45°;(2)、如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.
(1)、如图1,若∠ADB=90°,求证:∠DAH=45°;(2)、如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.