江苏省苏州吴江区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 点(﹣2，5)关于坐标原点对称的点的坐标是（）

A、(2，﹣5) B、(﹣2，﹣5) C、(2，5) D、(5，﹣2)

查看试题解析
3. 使二次根式 $\sqrt{x - 2}$ 有意义的x的取值范围是（）

A、x＞0 B、x＞2 C、x≥2 D、x≠2

查看试题解析
4.
如图，字母B所代表的正方形的面积是（　　）

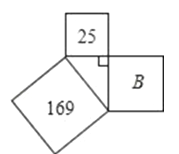A、12 B、144 C、13 D、194

查看试题解析
5. 如果△ABC≌△DEF，△DEF的周长为12，AB＝3，BC＝4，则AC的长为（）

A、2 B、3 C、4 D、5

查看试题解析
6. 若把分式 $\frac{x + y}{2 x}$ 中的x和y都扩大2倍，那么分式的值 $($ $)$

A、扩大2倍 B、不变 C、缩小2倍 D、缩小4倍

查看试题解析
7. 等腰三角形的一个角是80°，则它的顶角的度数是（）

A、80° B、80°或20° C、80°或50° D、20°

查看试题解析
8. 如图，已知直线 $y = 3 x 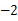+ b$ 与 $y = a x - 2$ 的交点的横坐标为，根据图象有下列3个结论：① $a > 0$ ；② $b < 0$ ；③ $x > - 2$ 是不等式 $3 x + b > a x - 2$ 的解集其中正确的个数是（）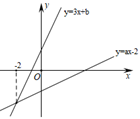

A、0， B、1， C、2， D、3

查看试题解析
9. 如图，在平面直角坐标系中，以点O为圆心，适当长为半径画弧交x轴于点M，交y轴于点N，再分别以点M，N为圆心，大于 $\frac{1}{2} MN$ 的长为半径画弧，两弧在第二象限交于点P，若点P的坐标为 $(4 a ， 3 b - 1)$ ，则a与b的数量关系为 $($ $)$

A、 $4 a - 3 b = 1$ B、 $4 a + b = 1$ C、 $4 a - b = 1$ D、 $4 a + 3 b = 1$

查看试题解析
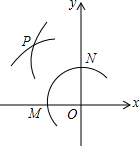10. 如图， $∠ BAC = 30^{\circ}$ ，AP平分 $∠ BAC$ ，GF垂直平分AP，交AC于F，Q为射线AB上一动点，若PQ的最小值为3，则AF的长为 $($ $)$

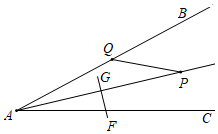A、3 B、6 C、 $3 \sqrt{3}$ D、9

查看试题解析

二、解答题

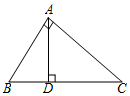
11. 化简计算：

(1)、化简： $\frac{3 a}{b} \cdot \frac{{ab}^{2}}{a^{3} b^{2}} \div \frac{6 b}{a^{2}}$ .

(2)、计算： $| 1 - \sqrt{2} | - \sqrt{{(- 2)}^{2}} - {(π - 3.14)}^{0}$ .

查看试题解析
12. 某中学组织学生去离学校15km的农场，先遣队与大队同时出发，先遣队的速度是大队的速度的1.2倍，结果先遣队比大队早到0.5h，先遣队和大队的速度各是多少？

查看试题解析
13. 如图，在 $△ ABC$ 中， $∠ BAC = 90^{\circ}$ ， $AB = 6$ ， $AC = 8$ ， $AD ⊥ BC$ ，垂足为D，求BC，AD的长.

查看试题解析
14. 操作探究： $△ ABC$ 在平面直角坐标系中的位置如图所示，其中 $A (- 3 ， 5)$ ， $B (- 5 ， 2)$ ， $C (- 1 ， 3)$ ，直线l经过点 $(0 ， 1)$ ，并且与x轴平行， $△ A'B'C'$ 与 $△ ABC$ 关于线l对称

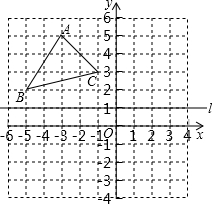(1)、画出 $△ A'B'C'$ ，并写出 $△ A'B'C'$ 三个顶点的坐标；

(2)、观察图中对应点坐标之间的关系，写出点 $P (a ， b)$ 关于直线l的对称点 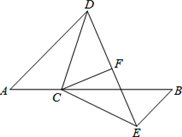$P'$ 的坐标.

查看试题解析
15. 如图，点 $C$ 在线段 $A B$ 上， $A D / / E B$ ， $A C = B E$ ， $A D = B C$ . $C F$ 平分 $∠ D C E$ .

求证：

(1)、 $△ A C D ≅ △ B E C$ ；

(2)、 $C F ⊥ D E$ .

查看试题解析
16. 初二 $(1)$ 班同学从学校出发去某自然保护区研学旅行，一部分乘坐大客车先出发，余下的几人20分钟后乘坐小轿车沿同一路线出行 $.$ 大客车中途停车等候，小轿车赶上来之后，大客车以出发时速度的 $\frac{10}{7}$ 继续行驶，小轿车保持原速度不变 $.$ 小轿车司机因路线不熟错过了景点入口，再原路提速返回，恰好与大客车同时到达景点入口 $.$ 两车距学校的路程 $S ($ 单位：千米 $)$ 和行驶时间 $t ($ 单位：分钟 $)$ 之间的函数关系如图所示.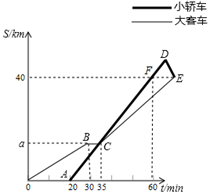

请结合图象解决下面问题：

(1)、学校到景点的路程为千米，大客车途中停留了分钟， $a =$ 千米；

(2)、在小轿车司机驶过景点入口时，大客车离景点入口还有多远？

(3)、若大客车一直以出发时的速度行驶，中途不再停车，那么小轿车折返后到达景点入口，需等待分钟，大客车才能到达景点入口.

查看试题解析
17. 如图，在平面直角坐标系中，一次函数 $y = kx + b$ 的图象与y轴的正半轴交于点A，与x轴交于点 $B (- 2 ， 0)$ ， $△ ABO$ 的面积为 $2.$ 动点P从点B出发，以每秒1个单位长度的速度在射线BO上运动，动点Q从O出发，沿x轴的正半轴与点P同时以相同的速度运动，过P作 $PM ⊥ X$ 轴交直线A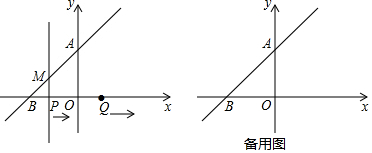B于M.

(1)、求直线AB的解析式.

(2)、当点P在线段OB上运动时，设 $△ MPQ$ 的面积为S，点P运动的时间为t秒，求S与t的函数关系式 $($ 直接写出自变量的取值范围 $)$ .

(3)、过点Q作 $QN ⊥ x$ 轴交直线AB于N，在运动过程中 $(P$ 不与B重合 $)$ ，是否存在某一时刻 $t ($ 秒 $)$ ，使 $△ MNQ$ 是等腰三角形？若存在，求出时间t值.

查看试题解析