江苏省苏州市昆山市2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-03 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x - 3}{x + 3}$ 的值为0，则x的值为 $($ $)$

A、3 B、 $- 3$ C、3或 $- 3$ D、0

查看试题解析
2. 如果y=(m-1) $x^{2 - m^{2}}$ +3是一次函数，那么m的值是（）

A、1 B、 $- 1$ C、 $\pm 1$ D、 $\pm \sqrt{2}$

查看试题解析
3. 某校九(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示，下面说法正确的是（）

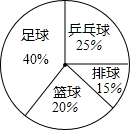A、从图中可以直接看出喜欢各种球类的具体人数 B、从图中可以直接看出全班的总人数 C、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 D、从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系

查看试题解析
4. 下列各数中，最大的数是（）

A、 $3 \sqrt{3}$ B、2 C、5 D、 $\sqrt{15}$

查看试题解析
5. 在平面直角坐标系中，点P(－2，x²＋1)所在的象限是( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 若式子 $\sqrt{k - 2} + {(2 - k)}^{0}$ 有意义，则一次函数y＝（2﹣k）x+k﹣2的图象可能是（）

A、 B、 C、 D、

查看试题解析
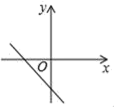7. 如图，直线y₁=k₁x+b和直线y₂=k₂x+b分别与x轴交于A(-1，0)和B(3，0)两点，则不等式组 ${\begin{matrix} k_{1} x + b > 0 \\ k_{2} x + b > 0 \end{matrix}$ 的解集为（）

A、 $- 1 < x < 3$ B、 $0 < x < 3$ C、 $- 1 < x < 0$ D、 $x > 3$ 或 $x < - 1$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，CD为AB边上的高，CE为AB边上的中线，AD=2，CE=5，则CD=（）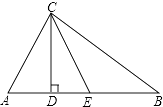

A、2 B、3 C、4 D、2 $\sqrt{3}$

查看试题解析
9. 设a＞b＞0，a²+b²=4ab，则 $\frac{a + b}{a - b}$ 的值为（）

A、3 B、 $\sqrt{6}$ C、2 D、 $\sqrt{3}$

查看试题解析
10. 如图（1），四边形ABCD中，AB∥CD，∠ADC＝90°，P从A点出发，以每秒1个单位长度的速度，按A→B→C→D的顺序在边上匀速运动，设P点的运动时间为t秒，△PAD的面积为S，S关于t的函数图象如图（2）所示，当P运动到BC中点时，△APD的面积为（）

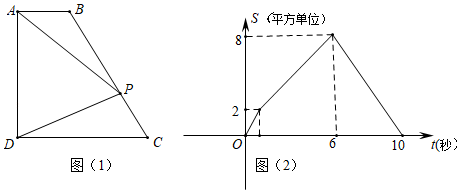A、4 B、5 C、6 D、7

查看试题解析

二、填空题

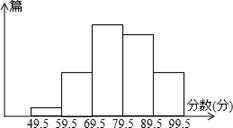
11. 若分式 $\frac{1}{2 x + 3}$ 在实数范围内有意义，则实数x的取值范围是.

查看试题解析
12. 点P(-3，5)关于y轴的对称点的坐标是.

查看试题解析
13. 已知：x：y：z=2：3：4，则 $\frac{x + 2 y - z}{x - y + 3 z}$ 的值为.

查看试题解析
14. 某校在“数学小论文“评比活动中，共征集到论文100篇，对论文评比的分数(分数为整数)整理后，分组画出频数分布直方图(如图)，已知从左到右5个小长方形的高的比为1：3：7：6：3，那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有篇.

查看试题解析
15.
含45 $° 角的$ 直角三角板如图放置在平面直角坐标系中，其中A（-2，0）、B（0，1），则直线BC的解析式为．

查看试题解析
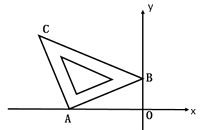16. 若x²-4x+1=0，则 $x^{2} + \frac{1}{x^{2}}$ =.

查看试题解析
17. 一次函数y=kx+3的图象与坐标轴的两个交点之间的距离为5，则k的值为.

查看试题解析
18. 在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为(3， $\sqrt{3}$ )，点C的坐标为(1，0)，点P为斜边OB上的一动点，则PA+PC的最小值.

查看试题解析

三、解答题

19. 计算

(1)、(- $\sqrt{3}$ )×(- $\sqrt{6}$ )- $\sqrt[3]{- 8}$ -(-2 $\sqrt{2}$ )²；

(2)、 $\frac{3}{2} \sqrt{x^{3}}$ +6x $\sqrt{\frac{x}{9}}$ -x² $\sqrt{\frac{1}{4 x}}$ .

查看试题解析
20. 先化简，再求值： $(x - 2 - \frac{12}{x + 2}) \div \frac{4 - x}{x + 2}$ ，其中 $x = - 4 + \sqrt{3}$ .

查看试题解析

21. 某乒乓球的质量检验结果如下：

抽取的乒乓球数n	50	100	200	500	1000	1500	2000
优等品的频数m	48	95	188	x	948	1426	1898
优等品的频率 $\frac{m}{n}$ (精确到0.001)	0.960	y	0.940	0.944	z	0.951	0.949

(1)、根据表中信息可得：x= ， y= ， z=；

(2)、从这批乒乓球中，任意抽取一只乒乓球是优等品的概率的估计值是多少？(精确到0.01).

查看试题解析

22. 如图，在7×7网格中，每个小正方形的边长都为1.

(1)、建立适当的平面直角坐标系后，若点A(1，3)、C(2，1)，则点B的坐标为；

(2)、△ABC的面积为；

(3)、判断△ABC的形状，并说明理由.

查看试题解析
23. 在△ABC中，AB=AC，D，E分别是AC，AB上的点，BE=CD，BD交CE于O.
求证：△OBC为等腰三角形.

查看试题解析
24. 如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，BC=10.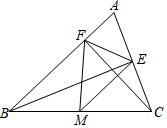

(1)、若∠ABC=50°，∠ACB=60°，求∠EMF的度数；

(2)、若EF=4，求△MEF的面积.

查看试题解析
25. 如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4 $\sqrt{5}$ ， $\frac{OC}{OA} = \frac{1}{2}$

(1)、求AC所在直线的解析式；

(2)、将纸片OABC折叠，使点A与点C重合(折痕为EF)，求折叠后纸片重叠部分的面积.

(3)、求EF所在的直线的函数解析式.

查看试题解析
26. 若一个三角形的三边长分别为a、b、c，设p= $\frac{1}{2}$ (a+b+c).
记：Q= $\sqrt{p (p - a) (p - b) (p - c)}$ .

(1)、当a=4，b=5，c=6时，求Q的值；

(2)、当a=b时，设三角形面积为S，求证：S=Q.

查看试题解析
27. 甲、乙两人相约元旦登山，甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图象如图所示，根据图象所提供的信息解答下列问题：

(1)、t=min.

(2)、若乙提速后，乙登山的上升速度是甲登山的上升速度3倍，
①求甲登山的上升速度

②请求出甲登山过程中，距地面的高度y(m)与登山时间x(min)之间的函数关系式.

③当甲、乙两人距地面高度差为70m时，求x的值(直接写出满足条件的x值).

查看试题解析
28. 已知：如图，一次函数y= $\frac{3}{4}$ x+3的图象分别与x轴、y轴相交于点A、B，且与经过点C(2，0)的一次函数y=kx+b的图象相交于点D，点D的横坐标为4，直线CD与y轴相交于点E.

(1)、直线CD的函数表达式为；(直接写出结果)

(2)、在x轴上求一点P使△PAD为等腰三角形，直接写出所有满足条件的点P的坐标.

(3)、若点Q为线段DE上的一个动点，连接BQ.点Q是否存在某个位置，将△BQD沿着直线BQ翻折，使得点D恰好落在直线AB下方的y轴上？若存在，求点Q的坐标；若不存在，请说明理由.

查看试题解析