湖北省武汉市黄陂区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下列手机APP图案中，属于轴对称的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x}{x - 1}$ 有意义，则x满足的条件是（）

A、x≠1 B、x≠－1 C、x≠0 D、x＝1

查看试题解析
3. 如图，在△ABC中，BD⊥AC交AC的延长线于点D，则AC边上的高是（）

A、CD B、AD C、BC D、BD

查看试题解析
4. 下列计算正确的是（）

A、b³ $\cdot$ b³＝2b³ B、(a⁵)²＝a⁷ C、x⁷÷x⁵＝x² D、(－2a)²＝－4a²

查看试题解析
5. 如图，五角星的五个角都是顶角为36°的等腰三角形，为了画出五角星，还需要知道∠ABC的度数，∠ABC的度数为（）

A、36° B、72° C、100° D、108°

查看试题解析
6. 工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C作射线OC，由做法得△MOC≌△NOC的依据是（）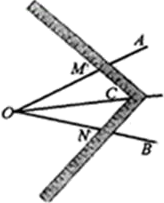

A、AAS B、SAS C、ASA D、SSS

查看试题解析
7. 下列因式分解错误的是（）

A、2ax－a＝a(2x－1) B、x²－2x＋1＝(x－1)² C、4ax²－a＝a(2x－1)² D、ax²＋2ax－3a＝a(x－1)(x＋3)

查看试题解析
8. 如图，一块直径为a＋b的圆形钢板，从中挖去直径分别为a与b的两个圆，则剩余阴影部分面积为（）

A、 $\frac{a b}{2}$ B、 $\frac{π {(a - b)}^{2}}{4}$ C、 $\frac{π a b}{2}$ D、 $\frac{π a b}{4}$

查看试题解析
9. 我们在过去的学习中已经发现了如下的运算规律：
( 1 )15×15＝1×2×100＋25＝225；(2)25×25＝2×3×100＋25＝625；(3)35×35＝3×4×100＋25＝1225；……按照这种规律，第n个式子可以表示为（）

A、n×n＝ $\frac{n - 5}{10}$ ×( $\frac{n - 5}{10}$ ＋1)×100＋25＝n² B、n×n＝ $\frac{n + 5}{10}$ ×( $\frac{n + 5}{10}$ ＋1)×100＋25＝n² C、(n＋5)×(n＋5)＝n×(n＋1)×100＋25＝n²＋10n＋25 D、(10n＋5)×(10n＋5)＝n×(n＋1)×100＋25＝100n²＋100n＋25

查看试题解析
10. 如图，四边形ABCD中，AB＝AD，BC＝BD，若∠ABD＝ $\frac{1}{2}$ ∠BAC＝a，则∠BDC的度数为（）

A、2a B、45°＋ $\frac{1}{2}$ a C、90°－a D、180°－3a

查看试题解析

二、填空题

11. 计算：2x² $\cdot$ 3xy＝.

查看试题解析
12. 平面直角坐标系中，点M(－2，1)关于x轴对称点N的坐标为.

查看试题解析
13. 用科学记数法表示：0.0012=；

查看试题解析
14. 甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个零件所用的时间与乙做60个零件所用的时间相等.设甲每小时做x个零件，依题意列方程为.

查看试题解析
15. 在Rt△ABC中，∠ACB＝90°，AC＝BC，过点C作直线CP，点A关于直线CP的对称点为D，连接AD.若∠ACP＝15°，则∠BAD的度数为.

查看试题解析
16. 如图，在△ABC中，AB＝AC，BD⊥AC于D，E为BD延长线上一点，∠E＝∠C，∠BAC的平分线交BD于F.若 $\frac{B D}{D E}$ ＝ $\frac{9}{4}$ ，则 $\frac{A D}{C D}$ 的值为.

查看试题解析

三、解答题

17. 解方程

(1)、 $\frac{1}{x}$ ＝ $\frac{2}{x - 3}$

(2)、 $\frac{x}{x - 1}$ － $\frac{3}{x + 1}$ ＝1

查看试题解析
18. 如图，已知△ABC≌△ $A^{'} B^{'} C^{'}$ ，AD， $A^{'} D^{'}$ 分别是△ABC，△ $A^{'} B^{'} C^{'}$ 的对应边上的高.
求证：AD＝ $A^{'} D^{'}$ .

查看试题解析
19. 因式分解

(1)、ax²－4a

(2)、(p－3)(p－1)＋1

查看试题解析
20. 计算

(1)、 $\frac{6 a b^{2}}{5 c} \cdot \frac{10 c}{3 b}$

(2)、( $\frac{x + 2}{x^{2} - 3 x}$ － $\frac{x - 3}{x^{2} - 6 x + 9}$ )÷ $\frac{x}{x - 3}$

查看试题解析
21. 如图，平面直角坐标系中，A(－2，1)，B(－3，4)，C(－1，3)，过点(l，0)作x轴的垂线 $l$ .

(1)、作出△ABC关于直线 $l$ 的轴对称图形△ $A^{'} B^{'} C^{'}$ ；

(2)、直接写出A₁( ， )，B₁( ， )，C₁( ， )；

(3)、在△ABC内有一点P(m，n)，则点P关于直线 $l$ 的对称点P₁的坐标为( ， )(结果用含m，n的式子表示).

查看试题解析
22. 某工地有72m²的墙面需要粉刷.若安排4名一级技工粉刷一天，结果还剩12m²墙面未能刷完；同样时间内安排6名二级技工去粉刷，则刚好全部刷完.已知每名一级技工比二级技工一天多粉刷3m²墙面.设每一名一级技工一天粉刷墙面xm².

(1)、每名二级技工一天粉刷墙面m²(用含x的式子表示)；

(2)、求每名一级技工、二级技工一天分别能粉刷多少m²墙面？

(3)、每名一级技工一天的施工费是300元，每名二级技工一天的施工费是200元.若另一工地有540m²的墙面需要粉刷，要求一天完工且施工总费用不超过10600元，则至少需要名二级技工(直接写出结果).

查看试题解析
23. 如图，在△ABC中，∠BAC＝60°，D为AB上一点，连接CD.

(1)、如图1，若∠BCA＝90°，CD⊥AB，则 $\frac{A D}{B D}$ ＝(直接写出结果).

(2)、如图2，若BD＝AC，E为CD的中点，AE与BC存在怎样的数量关系，判断并说明理由；

(3)、如图3，CD平分∠ACB，BF平分∠ABC，交CD于F.若BF＝AC，求∠ACD的度数.

查看试题解析
24. 在平面直角坐标系中，点A(a，0)，B(0，b)，且a，b满足a²－2ab＋b²＋(b－4)²＝0，点C为线段AB上一点，连接OC.

(1)、直接写出a＝， b＝；

(2)、如图1，P为OC上一点，连接PA，PB.若PA＝B0，∠BPC＝30°.求点P的纵坐标；

(3)、如图2，在(2)的条件下，点M是AB上一动点，以OM为边在OM的右侧作等边△OMN，连接CN.若OC＝t，求ON＋CN的最小值(结果用含t的式子表示).

查看试题解析