浙江省台州市三门县2017年八年级下学期期末数学试卷
试卷更新日期:2017-08-01 类型:期末考试
一、选择题
-
1. 如果 在实数范围内有意义,则x的取值范围是( )A、x≠4 B、x≤4 C、x≥4 D、x<42. 一次函数y=x+1不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 以下是期中考试后,八(1)班里两位同学的对话,小辉:“我们小组成绩是85分的人最多。”小聪:“我们小组7位同学成绩排在最中间的恰好也是85分。”以上两位同学的对话反映出的统计量是( )A、众数和方差 B、平均数和中位数 C、众数和平均数 D、众数和中位数4. 某地需要开辟一条隧道,隧道AB长度无法直接测量。如图所示,在地面上取一点C,使点C均可直接到达A、B两点,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )
 A、3300m B、2200m C、1100m D、550m5. 在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,则下列条件中:①a=10,b=8,c=6;②a2=3,b2=4,c2=5;③a2=(b+c)(b-c);④∠A=2∠B=2∠C。其中能判断△ABC是直角三角形的有( )
A、3300m B、2200m C、1100m D、550m5. 在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,则下列条件中:①a=10,b=8,c=6;②a2=3,b2=4,c2=5;③a2=(b+c)(b-c);④∠A=2∠B=2∠C。其中能判断△ABC是直角三角形的有( )
A、1个 B、2个 C、3个 D、4个6. 方程 经过配方后,其结果正确的是( )A、 B、 C、 D、7.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
 A、平行四边形 B、矩形 C、菱形 D、正方形8. 如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )A、m>0,n>0 B、m>0,n<0 C、m<0,n>0 D、m<0,n<09.
A、平行四边形 B、矩形 C、菱形 D、正方形8. 如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )A、m>0,n>0 B、m>0,n<0 C、m<0,n>0 D、m<0,n<09.如图,△ABC中,∠ACB=90°,∠A=25°,点D为斜边AB上的中点,DE⊥CD交AC于点E,则∠AED的度数为( )
 A、105° B、110° C、115° D、125°10.
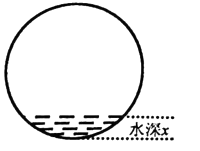
A、105° B、110° C、115° D、125°10.如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深间的函数关系的图象可能是( )
 A、
A、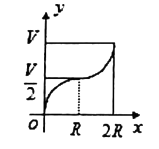 B、
B、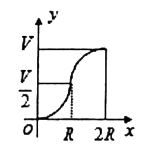 C、
C、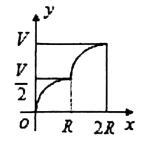 D、
D、
二、填空题
-
11. 方程(x-1)(x+2)=0的解为。12. 从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为: ,则小麦长势比较整齐的试验田是(填“甲”或“乙”)。13. 如图,AC、BD是菱形ABCD的两条对角线,若AD=5,AC=8,则BD的长是。
 14. 某中学规定学生的学期体育总评成绩满分为100分,其中平时成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩依次为95,90,88,则小彤这学期的体育总评成绩为。15. 如图,直线y=-x与y=ax+3a(a≠0)的交点的横坐标为-1.5,则关于x的不等式-x>ax+3a>0的整数解为。
14. 某中学规定学生的学期体育总评成绩满分为100分,其中平时成绩占20%,期中考试成绩占30%,期末考试成绩占50%,小彤的三项成绩依次为95,90,88,则小彤这学期的体育总评成绩为。15. 如图,直线y=-x与y=ax+3a(a≠0)的交点的横坐标为-1.5,则关于x的不等式-x>ax+3a>0的整数解为。 16. 如图,有一块平行四边形纸片ABCD,现将其折叠,使得AB落在AD上点F处,折痕为AE,再将△AEF沿EF翻折,若点A刚好落在CD边上点G处,则 =。
16. 如图,有一块平行四边形纸片ABCD,现将其折叠,使得AB落在AD上点F处,折痕为AE,再将△AEF沿EF翻折,若点A刚好落在CD边上点G处,则 =。
三、解答题
-
17. 计算:(1)、(2)、18. 已知关于x的方程 =0.
(1)、求证:不论a取何实数,该方程都有两个不相等的实数根。(2)、当a=1时,求该方程的根。19.如图,在△ABC中,AB=AC,D为边BC的中点,以AB、BD为邻边作平行四边形ABDE,连接AD、EC。
求证:四边形ADCE是矩形。
 20. 图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上。
20. 图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上。 (1)、如图1,作出以AB为对角线的正方形;(2)、如图2,以线段EF为一边作出菱形EFGH(不是正方形),点G、H在小正方形顶点处。21. 国家规定“中小学生每天在校体育活动时间不低于1小时”,为了解学生参加体育活动的情况。调查了某校八年级甲、乙两班学生每天参加体育锻炼的时间,并将调查结果制成如下的频数分布表和频数分布直方图(数据包括左端点不包括右端点)。
(1)、如图1,作出以AB为对角线的正方形;(2)、如图2,以线段EF为一边作出菱形EFGH(不是正方形),点G、H在小正方形顶点处。21. 国家规定“中小学生每天在校体育活动时间不低于1小时”,为了解学生参加体育活动的情况。调查了某校八年级甲、乙两班学生每天参加体育锻炼的时间,并将调查结果制成如下的频数分布表和频数分布直方图(数据包括左端点不包括右端点)。甲班学生每天参加体育活动时间频数分布表
分组(单位:h)
频数
0≤t<0.5
2
0.5≤t<1
10
1≤t<1.5
14
1.5≤t<2
12
2≤t<2.5
2
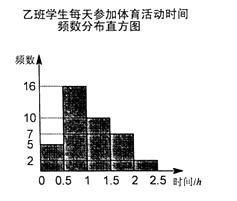
请你根据图表所提供的信息解答下列问题:
(1)、如果每天在校体育活动时间不低于1小时为“达标”,求甲班学生每天在校体育活动时间的达标率。(2)、乙班学生每天参加体育活动时间的中位数落在在哪一组?(3)、请选择一个适当的统计量,对甲、乙两班学生每天参加体育活动的时间进行评价。22. 我县为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题: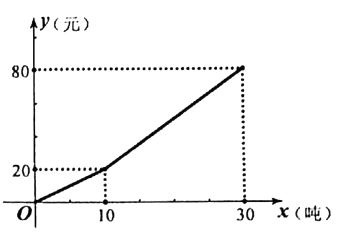 (1)、当用水量不超过10吨时,每吨水收费多少元?(2)、当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;(3)、某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。23. 在平面直角坐标系xOy中,点A(x1 , y1),B(x2 , y2),若x1x2+y1y2=0,则称A和B互为正交点,即A叫做B的正交点,B也叫做A的正交点。例如:A(1,1),B(2,-2),有1×2+1×(-2)=0,故A和B互为正交点。
(1)、当用水量不超过10吨时,每吨水收费多少元?(2)、当用水量超过10吨且不超过30吨时,求y与x之间的函数关系式;(3)、某户居民三、四月份水费共82元,四月份用水比三月份多4吨,求这户居民三月份用水多少吨。23. 在平面直角坐标系xOy中,点A(x1 , y1),B(x2 , y2),若x1x2+y1y2=0,则称A和B互为正交点,即A叫做B的正交点,B也叫做A的正交点。例如:A(1,1),B(2,-2),有1×2+1×(-2)=0,故A和B互为正交点。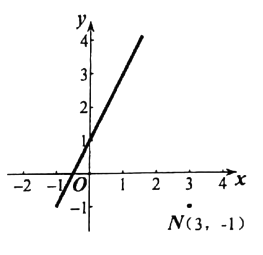 (1)、在直角坐标系xOy中,O为坐标原点,判断下列说法是否正确(对的写“正确”,错的写“错误”)。
(1)、在直角坐标系xOy中,O为坐标原点,判断下列说法是否正确(对的写“正确”,错的写“错误”)。①原点是任意点的正交点。
②x轴上的任意点与y轴上的任意点都互为正交点。
③点M和N互为正交点,则∠MON=90°.
④点M和N互为正交点,则OM=ON。
(2)、点P和Q互为正交点,P的坐标为(2,-3),Q的坐标为(6,m),求m的值。(3)、点M是直线y=2x+1上的一点,点M和N(3,-1)互为正交点,求MN的长度。24. 小明同学在做作业时,遇到如下问题:如图1,已知:等边△ABC,点D在BC上,以AD为边作等边△ADE,连接CE,求证:∠ACE=60°. (1)、请你解答小明的这道题;(2)、在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?
(1)、请你解答小明的这道题;(2)、在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?(直接答“是”或“不是”)
(3)、如图2,正方形ABCD的边长为2,E是直线BC上的一个动点,以DE为边作正方形DEFG(DEFG按逆时针排列)。当E在直线BC上运动时,点G是否在一条直线上运动?如果是,请你画出这条直线并证明;如果不是,也请说明理由;(4)、连接AG、CG,①求证:AG2-CE2是定值; ②求AG+CG的最小值(直接写出答案即可)。