2016-2017学年浙江省椒江区数学八年级下学期期末考试

试卷更新日期：2017-08-01 类型：期末考试

进入出卷网下载

一、选择题

1. 下列式子一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt[3]{6}$ C、 $\sqrt{5}$ D、 $\sqrt{2 x}$

查看试题解析
2. 二次根式的除法法则 $\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$ 成立的条件是（）

A、a>0,b>0 B、a≥0,b>0 C、a≥0,b≥0 D、a≤0,b<0

查看试题解析
3. 一次函数 $y = - \frac{1}{2} x + 1$ 的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 台州市椒江区位于浙江沿海中部台州湾入口处，属于严格热带季风区，受海洋水体调节，气候温和湿润，四季分明，夏天酷暑而冬天奇寒.下表是2016上半年椒江区各月雨天的天数：
月份
1月
2月
3月
4月
5月
6月
雨天数（天）
5
9
10
14
12
9
雨天天数的众数和中位数分别（）

A、9, 9.5 B、9.5, 9 C、9,9 D、10,9

查看试题解析
5. 分别以下列各组数一个三角形的三边长，其中能构成直角三角形的是（）

A、 $\sqrt{3}, \sqrt{4}, \sqrt{5}$ B、 $1, 2, \sqrt{3}$ C、 $\frac{1}{3}, \frac{1}{4}, \frac{1}{5}$ D、2,3,4

查看试题解析
6.
水龙头关闭不严会造成滴水，为了调查漏水量与漏水时间的关系，可在滴水的水龙下放置一个水杯，每5分钟称一次水杯的重，如下表：
时间t(分)
15
20
25
…
重量w(克)
65
80
95
…
若水杯的重量w是滴水时间t的一次函数，则滴水时间为32分时，水杯的重量为（）

A、107克 B、110克 C、113克 D、116克

查看试题解析
7. 下列命题中正确的命题是（）

A、两条对角线互相垂直的矩形是正方形 B、有一个角是直角的四边形是矩形 C、平行四边形是轴对称图形 D、两条对角线相等的平行四边形是菱形

查看试题解析
8.
如图，圆柱的底面圆的周长为6cm，高4cm，一只蚂蚁沿外壁从A点爬行到B点，则最少要爬行（）

A、10cm B、4 $\sqrt{13}$ cm C、5cm D、2 $\sqrt{10}$ cm

查看试题解析
9.
小明某一天放学从学校回家，如图，大致描述他回家过程中离家的距离S(千米)与所用时间t(分)之间的关系，下列说法错误的是（）

A、学校离家距离为2千米 B、前4分钟，小明平均速度为200米/分钟 C、骑了4分钟后，小明加快了速度 D、骑了4分钟时，小明离学校1.2千米

查看试题解析
10.
如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，分别以直角三角形三边AB、AC、BC向外作正方形ABFE、正方形ACNM、正方形BCPQ，连接EM，则EM的长度为（）

A、 $\sqrt{65}$ B、 $\sqrt{73}$ C、 $3 \sqrt{10}$ D、 $\sqrt{97}$

查看试题解析

二、填空题

11. 计算 $\sqrt{2} \times \sqrt{3}$ =.

查看试题解析
12. 在▱ABCD中，若∠A+∠C=260°，则∠B的度数为.

查看试题解析
13.
如图，利用函数图象求不等式2x>kx+b的解集为.

查看试题解析
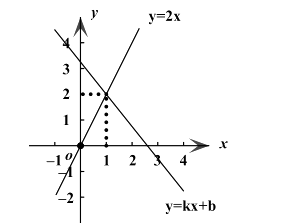14. 意大利数学家斐波那契研究了一列非常奇妙的数，被称为斐波那契数列，斐波那契数列中的第n个数可以用 $\frac{1}{\sqrt{5}}$ $[{(\frac{1 + \sqrt{5}}{2})}^{n} - {(\frac{1 - \sqrt{5}}{2})}^{n}]$ 表示（其中，n≥1）.这是用无理数表示有理数的一个范例，斐波那契数列中的第2个数可化简为.

查看试题解析
15.
如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处，若AB=6cm，AC=10cm，则四边形AECF的面积为cm².

查看试题解析
16.
如图1，在▱ABCD中，设∠ABC=α，▱ABCD的面积为s，s与α之间的关系如图2所示，则m=.

查看试题解析

三、解答题

17. 计算： $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$ .

查看试题解析
18. 已知 $y = \sqrt{2 x - 5} - \sqrt{5 - 2 x} + 3$ ，求 $(2 \sqrt{x} + \sqrt{y}) (2 \sqrt{x} - \sqrt{y})$ 的值.

查看试题解析
19.
如图，矩形ABCD的对角线AC与BD相交于点O，CE//BD，DE//AC.

(1)、求证：四边形OCED是菱形；

(2)、当CD=6，DE=5，求AD的长.

查看试题解析
20. 某校八（1）班开展男生、女生垫排球比赛活动，每队各派5名同学参加.下表是男生队和女生队5名同学的比赛数据（单位：个）：

1号
2号
3号
4号
5号
男生队
100
98
110
89
103
女生队
88
100
95
120
97
请回答下列问题：

(1)、计算两队的平均成绩；

(2)、从成绩稳定性角度考虑，哪队成绩稍好，请说明理由.

查看试题解析
21. 台州市某体育用品商店一次性购进排球、足球两种商品共100个，排球每个进价40元，售价50元，足球每个进价90元，售价105元.

(1)、设购进排球x个，销售完此两种商品的总利润为y元，求出y与x的函数关系式；

(2)、该商家计划最多投入8000元用于购进此两种商品共100件，至少要购进多少个排球？

(3)、在（2）的条件下，若售完这些商品，商家可获得最大利润是多少元？

查看试题解析
22.
两组邻边分别相等的四边形叫做筝形.如图1，四边形ABCD是一个筝形，其中AD=CD，AB=CB，我们称这个四边形是“筝形ABCD”.

(1)、根据筝形的定义判断下列命题是否正确，真命题打“√”，假命题打“×”.
①筝形有一组对角相等.
②菱形是筝形.
③筝形的面积为两条对角线长度的乘积.

(2)、如图2，有一个公共顶点B的两个正方形ABCD与正方形BEFG全等，边AD与EF相交于点H.请你判断四边形BEHA是否是“筝形”，说明你的理由；

(3)、如图3，当∠EBC=30°时，延长DA交GF于点K.若正方形ABCD边长为 $\sqrt{3}$ ，求线段AK的长.

查看试题解析
23.
如图1，在平面直角坐标系xOy中，点P的坐标为（ $x_{1} ， y_{1}$ ），点Q的坐标为 $(x_{2} ， y_{2})$ ，且 $x_{1} \neq x_{2}$ ， $y_{1} \neq y_{2}$ ，若P，Q为某个矩形的两个顶点，且该矩形的一组对边与某条坐标轴平行，则称该矩形为点P，Q的“相关矩形”，图2及图3中点A的坐标为（4，3）.

(1)、若点B的坐标为（-2，0），则点A，B的“相关矩形”的面积为；

(2)、点C在y轴上，若点A，C的“相关矩形”的面积为8，求直线AC的解析式；

(3)、如图3，直线 $y = - \frac{1}{2} x + 2$ 与x轴交于点M，与y轴交于点N，在直线MN上是否存在点D，使点A，D的“相关矩形”为正方形，如果存在，请求出点D的坐标，如果不存在，请说明理由.

查看试题解析

	1号	2号	3号	4号	5号
男生队	100	98	110	89	103
女生队	88	100	95	120	97

月份	1月	2月	3月	4月	5月	6月
雨天数（天）	5	9	10	14	12	9

时间t(分)	15	20	25	…
重量w(克)	65	80	95	…