山西省大同市2019-2020学期高三上学期理数第一次联合考试试卷

试卷更新日期：2020-01-02 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知集合 $A = {y | y = \ln (x - 1)}$ ， $B = {x | x^{2} - 4 \leq 0}$ ，则 $A \cap B =$ （　　）

A、 ${x | x \geq - 2}$ B、 ${x | 1 < x < 2}$ C、 ${x | 1 < x \leq 2}$ D、 ${x | - 2 \leq x \leq 2}$

查看试题解析
2. 欧拉公式 $e^{i x} = \cos x + i \sin x$ （ $i$ 为虚数单位）是由瑞士著名数学家欧拉发现的，它将指数函数的定义域扩大到复数集，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位.特别是当 $x = π$ 时， $S_{n} + S_{n} - S_{n - 1} = 2 S_{n} - S_{n - 1} = \frac{1}{n + 1} - (\frac{1}{n} - \frac{1}{n + 1}) = \frac{2}{n + 1} - \frac{1}{n}$ 被认为是数学上最优美的公式，数学家们评价它是“上帝创造的公式”.根据欧拉公式可知， $e^{2 i}$ 表示的复数在复平面中位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 将函数 $y = \sin (2 x + \frac{π}{6})$ 的图象向左平移 $\frac{π}{6}$ 个单位长度后，所得图象的一个对称中心为（）

A、 $(\frac{π}{12} ， 0)$ B、 $(\frac{π}{4} ， 0)$ C、 $(\frac{π}{3} ， 0)$ D、 $(\frac{π}{2} ， 0)$

查看试题解析
4. 如图，在 $Δ A B C$ 中， $\vec{A N} = \frac{2}{3} \vec{N C}$ ， $P$ 是 $B N$ 上一点，若 $\vec{A P} = t \vec{A B} + \frac{1}{3} \vec{A C}$ ，则实数 $t$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{1}{6}$ D、 $\frac{3}{4}$

查看试题解析
5. 函数 $f (x) = 6^{| \sin x |} - \frac{x^{2}}{\sqrt{1 + x^{2}}}$ 的图象大致为（　　）

A、 B、 C、 D、

查看试题解析
6. 若 $f (x) = ln x$ 与 $g (x) = x^{2} + a x$ 两个函数的图象有一条与直线 $y = x$ 平行的公共切线，则 $a =$ （）

A、 $1$ B、 $2$ C、 $3$ D、 $3$ 或 $- 1$

查看试题解析
7. 已知定义域为 $R$ 的奇函数 $f (x)$ 满足 $f (3 - x) + f (x) = 0$ ，且当 $x \in (- \frac{3}{2}, 0)$ 时, $f (x) = \log_{2} (2 x + 7)$ ，则 $f (2020) =$ （　　）

A、 $- \log_{2} 5$ B、2 C、-2 D、 $\log_{2} 5$

查看试题解析
8. 已知 $a = \sqrt{2}$ , $b = \sqrt[5]{5}$ , $c = \sqrt[7]{7}$ ,则（）

A、 $a > b > c$ B、 $a > c > b$ C、 $b > a > c$ D、 $c > b > a$

查看试题解析
9. 已知正实数 $m, n$ 满足 $\frac{1}{m} + \frac{4}{n} = 4$ ，则 $m + n$ 的最小值是（）

A、2 B、4 C、9 D、 $\frac{9}{4}$

查看试题解析
10. 从装有若干个大小相同的红球、白球和黄球的袋中随机摸出1个球，摸到红球、白球和黄球的概率分别为 $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{6}$ ，从袋中随机摸出一个球，记下颜色后放回，连续摸3次，则记下的颜色中有红有白但没有黄的概率为（）

A、 $\frac{5}{36}$ B、 $\frac{1}{3}$ C、 $\frac{5}{12}$ D、 $\frac{1}{2}$

查看试题解析
11. 已知 $F$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的左焦点， $E$ 是双曲线的右顶点，过点 $F$ 且垂直于 $x$ 轴的直线与双曲线交于 $A, B$ 两点，若 $Δ A B E$ 是锐角三角形，则该双曲线的离心率 $e$ 的取值范围为（）

A、 $(1, 2)$ B、 $(1, \sqrt{2})$ C、 $(1, 3)$ D、 $(1, \sqrt{3})$

查看试题解析
12. 已知定义在 $R$ 上的可导函数 $f (x)$ ，对于任意实数 $x$ 都有 $f (- x) = f (x) - 2 x$ 成立，且当 $x \in (- \infty, 0]$ 时，都有 $f' (x) < 2 x + 1$ 成立，若 $f (2 m) < f (m - 1) + 3 m (m + 1)$ ，则实数 $m$ 的取值范围为（）

A、 $(- 1, \frac{1}{3})$ B、 $(- 1, 0)$ C、 $(- \infty, - 1)$ D、 $(- \frac{1}{3}, + \infty)$

查看试题解析

二、填空题

13. 命题 $p : \exists x_{0} \in (0, + \infty)$ , $x_{0}^{2} \leq x_{0} + 2$ ，则 $\neg p$ 是；

查看试题解析
14. 已知两个单位向量 $\vec{a}, \vec{b}$ 满足 $| \vec{a} + \vec{b} | = \sqrt{3} | \vec{b} |$ ，则 $\vec{a}, \vec{b}$ 的夹角为．

查看试题解析
15. 设数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n} = \frac{4}{3} a_{n} - \frac{1}{3} \times 2^{n + 1} + \frac{2}{3}$ ， $n = 1, 2, 3, \dots$ ，则 ${a_{n}}$ 的通项公式为 $a_{n} =$ ．

查看试题解析
16. 已知函数 $f (x) = {\begin{matrix} {log}_{4} x + x - 3 (x > 0), \\ x - {(\frac{1}{4})}^{x} + 3 (x \leq 0), \end{matrix}$ 若 $f (x)$ 的两个零点分别为 $x_{1}, x_{2}$ ，则 $| x_{1} - x_{2} | =$ ．

查看试题解析

三、解答题

17. 在 $Δ A B C$ 中， $a, b, c$ 分别为角 $A, B, C$ 的对边， $\cos (C + B) \cos (C - B) = \cos^{2} A - \sin C \sin B$

(1)、求 $A$ ；

(2)、若 $a = 3$ ，求 $b + 2 c$ 的最大值.

查看试题解析
18. 如图，四棱锥 $P - A B C D$ ， $A B / / C D$ ， $∠ B C D = 90 °$ ， $A B = 2 B C = 2 C D = 4$ ， $Δ P A B$ 为等边三角形，平面 $P A B ⊥$ 平面 $A B C D$ ， $Q$ 为 $P B$ 中点.

(1)、求证： $A Q ⊥$ 平面 $P B C$ ；

(2)、求二面角 $B - P C - D$ 的余弦值.

查看试题解析
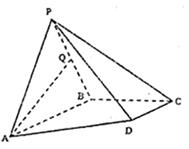19. 新高考改革后，国家只统一考试数学和语文，英语学科改为参加等级考试，每年考两次，分别放在每个学年的上、下学期，物理、化学、生物、地理、历史、政治这六科则以该省的省会考成绩为准.考生从中选择三科成绩，参加大学相关院系的录取.

(1)、若英语等级考试成绩有一次为优，即可达到某211院校的录取要求.假设某个学生参加每次等级考试事件是独立的，且该生英语等级考试成绩为优的概率都是 $\frac{1}{3}$ ，求该生在高二上学期的英语等级考试成绩才为优的概率；

(2)、据预测，要想报考该211院校的相关院系，省会考的成绩至少在90分以上，才有可能被该校录取.假设该生在省会考六科的成绩，考到90分以上概率都是 $\frac{1}{3}$ ，设该生在省会考时考到90分以上的科目数为 $ε$ ，求 $ε$ 的分布列及数学期望.

查看试题解析
20. 已知椭圆 $C$ 中心在原点，焦点在坐标轴上，直线 $y = \frac{3}{2} x$ 与椭圆 $C$ 在第一象限内的交点是 $M$ ，点 $M$ 在 $x$ 轴上的射影恰好是椭圆 $C$ 的右焦点 $F_{2}$ ，椭圆 $C$ 另一个焦点是 $F_{1}$ ，且 $\vec{M F_{1}} \cdot \vec{M F_{2}} = \frac{9}{4}$ .

(1)、求椭圆 $C$ 的方程；

(2)、直线 $l$ 过点 $(- 1, 0)$ ，且与椭圆 $C$ 交于 $P, Q$ 两点，求 $Δ F_{2} P Q$ 的内切圆面积的最大值.

查看试题解析
21. 设函数 $f (x) = 4 \ln x - \frac{1}{2} a x^{2} + (4 - a) x (a \in R)$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、若函数 $f (x)$ 存在极值，对于任意的 $0 < x_{1} < x_{2}$ ，存在正实数 $x_{0}$ ，使得 $f (x_{1}) - f (x_{2}) = f^{'} (x_{0}) \cdot (x_{1} - x_{2})$ ，试判断 $x_{1} + x_{2}$ 与 $2 x_{0}$ 的大小关系并给出证明.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，已知曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = 3 + 2 \cos φ \\ y = 2 \sin φ \end{array}$ （ $φ$ 为参数），以坐标原点 $O$ 为极点，以 $x$ 轴的正半轴为极轴，建立极坐标系，曲线 $C_{2}$ 的极坐标方程为 $ρ = 2$ .

(1)、设点 $M, N$ 分别为曲线 $C_{1}$ 与曲线 $C_{2}$ 上的任意一点，求 $| M N |$ 的最大值；

(2)、设直线 $l : {\begin{array}{l} x = - 1 + t \cos α \\ y = t \sin α \end{array}$ （ $t$ 为参数）与曲线 $C_{1}$ 交于 $P, Q$ 两点，且 $| P Q | = 1$ ，求直线 $l$ 的普通方程.

查看试题解析
23. 已知函数 $f (x) = | x + a | + | x - 1 |$ .

(1)、当 $a = 3$ 时，求不等式 $f (x) \geq x + 9$ 的解集；

(2)、若 $f (x) \leq | x - 4 |$ 的解集包含 $[0, 2]$ ，求实数 $a$ 的取值范围.

查看试题解析