浙江省义乌市三校2020届九年级上学期数学第三次月考试卷
试卷更新日期:2019-12-31 类型:月考试卷
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 下列函数中,是二次函数的是( )A、 B、 C、 D、2. 一个不透明的袋子中只装有5个红球,从中随机摸出一个球是黑球( )A、属于随机事件 B、可能性大小为 C、属于不可能事件 D、是必然事件3. 将抛物线y=x2向下平移1个单位,所得到的抛物线是( )A、y=(x-1)2 B、y=x2-1 C、y=(x+1)2 D、y=x2+14. 已知⊙O的半径为3,直线l上有一点P满足PO=3,则直线l与⊙O的位置关系是( )A、相切 B、相离 C、相离或相切 D、相切或相交5. 如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB:FG=2:3,则下列结论正确的是( )
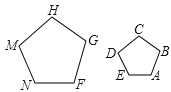 A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F6. 如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB= ,则⊙O的半径为( )
A、2DE=3MN B、3DE=2MN C、3∠A=2∠F D、2∠A=3∠F6. 如图,⊙O是△ABC的外接圆,弦AC的长为3,sinB= ,则⊙O的半径为( )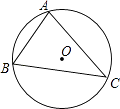 A、4 B、3 C、2 D、7. 已知反比例函数 的图象如图所示,则二次函数 的图象大致为( )
A、4 B、3 C、2 D、7. 已知反比例函数 的图象如图所示,则二次函数 的图象大致为( ) A、
A、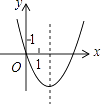 B、
B、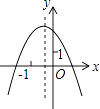 C、
C、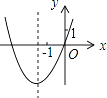 D、
D、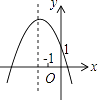 8. 如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数 的图象经过点A,反比例函数 的图象经过点B,则下列关于m,n的关系正确的是( )
8. 如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数 的图象经过点A,反比例函数 的图象经过点B,则下列关于m,n的关系正确的是( )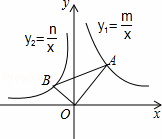 A、 B、 C、 D、9. 如图,正方形ABCD的边AB=1, 和 都是以1为半径的圆弧,则无阴影两部分的面积之差是( )
A、 B、 C、 D、9. 如图,正方形ABCD的边AB=1, 和 都是以1为半径的圆弧,则无阴影两部分的面积之差是( ) A、 B、1﹣ C、 ﹣1 D、1﹣10. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
A、 B、1﹣ C、 ﹣1 D、1﹣10. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:x
…
0
4
…
y
…
0.37
-1
0.37
…
则方程ax2+bx+1.37=0的根是( )
A、0或4 B、 或 C、1或5 D、无实根二、填空题(本题有6小题,每小题4分,共24分)
-
11. 已知 ,则 的值是 .12. 二次函数y=3x2﹣6x+2的图象的对称轴为 , 顶点坐标为 .13. 如果b=4是a与c的比例中项,且a=3,那么c= .14. 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD=.
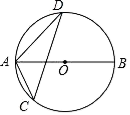 15. 如图,在扇形AOB中,∠AOB=90°,弧AC=弧BC,过点C作 CD⊥OB于点D,以CD为边向右作正方形CDEF,若OA= ,则阴影部分的面积是(结果保留π).
15. 如图,在扇形AOB中,∠AOB=90°,弧AC=弧BC,过点C作 CD⊥OB于点D,以CD为边向右作正方形CDEF,若OA= ,则阴影部分的面积是(结果保留π).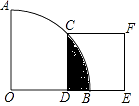 16. 在平面直角坐标系中,将函数 的图象绕坐标原点O顺时针旋转45°后,得到新曲线l.
16. 在平面直角坐标系中,将函数 的图象绕坐标原点O顺时针旋转45°后,得到新曲线l.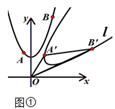
 (1)、如图①,已知点A(-1,a),B(b,10)在函数 的图象上,若 A', B'是A,B旋转后的对应点,连结OA', OB',则S△OA'B '=;(2)、如图②,曲线l与直线 相交于点M、N,则S△OMN为.
(1)、如图①,已知点A(-1,a),B(b,10)在函数 的图象上,若 A', B'是A,B旋转后的对应点,连结OA', OB',则S△OA'B '=;(2)、如图②,曲线l与直线 相交于点M、N,则S△OMN为.三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、(2)、计算:18. 如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
 19. 如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,-3).
19. 如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,-3).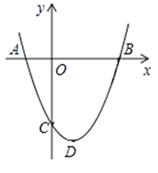 (1)、求该函数的解析式;(2)、求该抛物线与x轴的交点A,B的坐标.20.
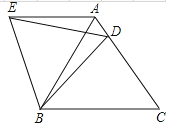
(1)、求该函数的解析式;(2)、求该抛物线与x轴的交点A,B的坐标.20.如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,求△AED的周长.
 21. 如图,Rt△ABC中,∠ACB=90°,cosA= ,D为AB上一点,且AD:BD=1:2,若BC=3 ,求CD的长.
21. 如图,Rt△ABC中,∠ACB=90°,cosA= ,D为AB上一点,且AD:BD=1:2,若BC=3 ,求CD的长.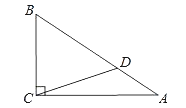 22. 某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).(1)、求y与x(x>20)的函数关系式;(2)、已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;(3)、在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入﹣接待成本)23. 如图,在平面直角坐标系中,点A、B、C、E、P均在坐标轴上,A(0,3)、B(﹣4,0)、P(0,﹣3),点C是线段OP(不包含O、P)上一动点,AB∥CE,延长CE到D,使CD=BA
22. 某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).(1)、求y与x(x>20)的函数关系式;(2)、已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;(3)、在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入﹣接待成本)23. 如图,在平面直角坐标系中,点A、B、C、E、P均在坐标轴上,A(0,3)、B(﹣4,0)、P(0,﹣3),点C是线段OP(不包含O、P)上一动点,AB∥CE,延长CE到D,使CD=BA (1)、如图,点M在线段AB上,连MD,∠MAO与∠MDC的平分线交于N.若∠BAO=α,∠BMD=130°,则∠AND的度数为;(2)、如图,连BD交y轴于F.若OC=2OF,求点C的坐标(3)、如图,连BD交y轴于F,在点C运动的过程中, 的值是否变化?若不变,求出其值;若变化,请说明理由.24. 如图1,在平面直角坐标系中,二次函数y=﹣ x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
(1)、如图,点M在线段AB上,连MD,∠MAO与∠MDC的平分线交于N.若∠BAO=α,∠BMD=130°,则∠AND的度数为;(2)、如图,连BD交y轴于F.若OC=2OF,求点C的坐标(3)、如图,连BD交y轴于F,在点C运动的过程中, 的值是否变化?若不变,求出其值;若变化,请说明理由.24. 如图1,在平面直角坐标系中,二次函数y=﹣ x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.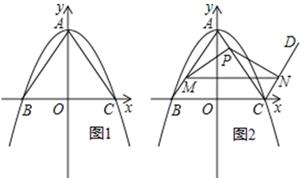 (1)、点B的坐标为 , 点C的坐标为;(2)、过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N (点 Q不与点P重合),连接PM,PN,设线段AP的长为n.
(1)、点B的坐标为 , 点C的坐标为;(2)、过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N (点 Q不与点P重合),连接PM,PN,设线段AP的长为n.①如图2,当n< AC时,求证:△PAM≌△NCP;
②直接用含n的代数式表示线段PQ的长;
③若PM的长为 ,当二次函数 的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.