浙江省宁波市奉化区2020届九年级上学期数学12月月考试卷
试卷更新日期:2019-12-31 类型:月考试卷
一、选择题(共12小题,4*12=48)
-
1. 若3x=2y(xy≠0),则下列比例式成立的是( )A、 B、 C、 D、2. 下列事件中属于必然事件的是( )A、任意买一张电影票,座位号是偶数 B、367人中至少有2人的生日相同 C、掷一次骰子,向上的一面是5点 D、某射击运动员射击1次,命中靶心3. 已知△ABC中,∠C=90°,若AC= ,BC=1,则sinA的值是( )A、 B、 C、 D、4. 如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
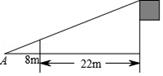 A、6m B、8.8m C、12m D、15m5. 一个点到圆的最大距离为9 cm,最小距离为3 cm,则圆的半径为( )A、3 cm或6 cm B、6 cm C、12 cm D、12 cm或6 cm6. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A、6m B、8.8m C、12m D、15m5. 一个点到圆的最大距离为9 cm,最小距离为3 cm,则圆的半径为( )A、3 cm或6 cm B、6 cm C、12 cm D、12 cm或6 cm6. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )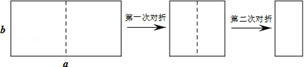 A、a= b B、a=2b C、a=2 b D、a=4b7. 下列有关圆的一些结论:①弦的垂直平分线经过圆心;②平分弦的直径垂直于弦;③相等的圆心角所对的两条弦的弦心距相等;④等弧所在的扇形面积都相等,其中正确结论的个数是( )A、4 B、3 C、2 D、18. 如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为4的“等边扇形”的面积为( )A、8 B、16 C、2π D、4π9. 如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是46°,则∠ACD的度数为( )
A、a= b B、a=2b C、a=2 b D、a=4b7. 下列有关圆的一些结论:①弦的垂直平分线经过圆心;②平分弦的直径垂直于弦;③相等的圆心角所对的两条弦的弦心距相等;④等弧所在的扇形面积都相等,其中正确结论的个数是( )A、4 B、3 C、2 D、18. 如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为4的“等边扇形”的面积为( )A、8 B、16 C、2π D、4π9. 如图,一块三角尺ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是46°,则∠ACD的度数为( ) A、46° B、23° C、44° D、67°10. 二次函数 y=ax2+bx+c(a≠0) 的图象如图所示,则一次函数 y=bx+b2-4ac 与反比例函数 y= 在坐标系内的图象大致为( )
A、46° B、23° C、44° D、67°10. 二次函数 y=ax2+bx+c(a≠0) 的图象如图所示,则一次函数 y=bx+b2-4ac 与反比例函数 y= 在坐标系内的图象大致为( )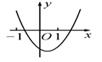 A、
A、 B、
B、 C、
C、 D、
D、 11. 如图:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
11. 如图:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )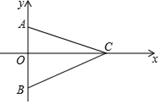 A、OC=12 B、△ABC外接圆的半径等于 C、∠BAC=60° D、△ABC外接圆的圆心在OC上12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①4a+2b+c>0;②abc<0;③b<a﹣c;④3b>2c;⑤a+b<m(am+b),(m≠1的实数);其中正确结论的个数为( )
A、OC=12 B、△ABC外接圆的半径等于 C、∠BAC=60° D、△ABC外接圆的圆心在OC上12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①4a+2b+c>0;②abc<0;③b<a﹣c;④3b>2c;⑤a+b<m(am+b),(m≠1的实数);其中正确结论的个数为( )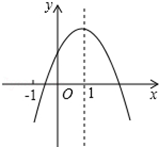 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(共6小题,4*6=24)
-
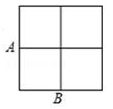
13. 已知线段a=4 cm,b=9 cm,则线段a,b的比例中项为cm.14. 将抛物线y=﹣x2向左平移2个单位后,得到的抛物线的解析式是 .15. 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是 .
16. 如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO= BE,则线段OD= , BE= . 17. 如图,在直线l上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC= CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1 , S2 , S3 , 若S1+S3=20,则S1= , S2= .
17. 如图,在直线l上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC= CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1 , S2 , S3 , 若S1+S3=20,则S1= , S2= .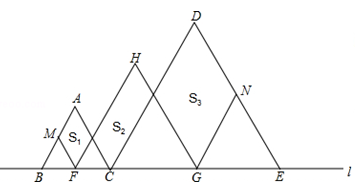 18. 如图,在△ABC中,已知AB=AC=5cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t= .
18. 如图,在△ABC中,已知AB=AC=5cm,BC=8 cm,点P在边BC上沿B到C的方向以每秒1cm的速度运动(不与点B,C重合),点Q在AC上,且满足∠APQ=∠B,设点P运动时间为t秒,当△APQ是等腰三角形时,t= .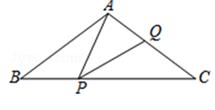
三、解答题(共8小题,66分)
-
19.(1)、计算: sin60°﹣ cos45°+tan230°;(2)、若 = = ≠0,求 的值.20. 在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.(1)、从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;(2)、在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.21. 如图,小山岗的斜坡AC的坡度是 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数)
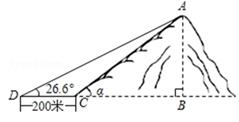
(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50).
22. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,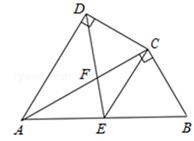 (1)、求证:AC2=AB•AD;(2)、求证:△AFD∽△CFE.23. 我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.(1)、试确定月销售量y(台)与售价x(元/台)之间的函数关系式和自变量x的范围;(2)、当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?24. 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)、求证:AC2=AB•AD;(2)、求证:△AFD∽△CFE.23. 我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.(1)、试确定月销售量y(台)与售价x(元/台)之间的函数关系式和自变量x的范围;(2)、当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?24. 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F. (1)、AB与AC的大小有什么关系?请说明理由;(2)、若AB=8,∠BAC=45°,求:图中阴影部分的面积.25. 定义:在一个三角形中,若存在两条边 x 和 y,使得 y = x2 ,则称此三角形为“平方三角形”,x 称为平方边.
(1)、AB与AC的大小有什么关系?请说明理由;(2)、若AB=8,∠BAC=45°,求:图中阴影部分的面积.25. 定义:在一个三角形中,若存在两条边 x 和 y,使得 y = x2 ,则称此三角形为“平方三角形”,x 称为平方边. (1)、若等边三角形为平方三角形,则面积为 是命题;
(1)、若等边三角形为平方三角形,则面积为 是命题;有一个角为 30°且有一条直角边为 2 的直角三角形是平方三角形”是命题;(填“真”或“假”)
(2)、若a,b,c 是平方三角形的三条边,平方边 a=2,若三角形中存在一个角为 60°, 求 c 的值;
(3)、如图,在△ABC 中,D 是 BC 上一点.①若∠CAD=∠B,CD=1,求证,△ABC 是平方三角形;
②若∠C=90°,BD=1,AC=m,CD=n,求tan∠DAB.(用含m,n的代数式表示)26. 如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1, 0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.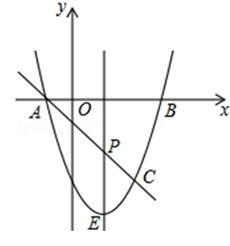 (1)、求抛物线的函数解析式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
(1)、求抛物线的函数解析式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.