浙江省杭州市萧山区城区片六校2019-2020学年八年级上学期数学12月月考试卷
试卷更新日期:2019-12-31 类型:月考试卷
一、选择题(本大题有10小题,每小题3分,共30分)
-
1. 根据下列表述,能够确定一物体位置的是( )A、东北方向 B、萧山歌剧院8排 C、朝晖大道 D、东经20度北纬30度2. 若a>b,则下列各式中一定成立的是( )A、ma﹥mb B、a2﹤b2 C、1-a﹥1-b D、b-a﹤03. 已知等腰△ABC的周长为18cm,BC=8cm,若△ABC与△A′B′C′全等,则△A′B′C′的腰长等于( )A、8cm B、2cm或8cm C、5cm D、8cm或5cm4. 已知点M(a,2),B(3,b)关于y轴对称,则a+b=( )A、-5 B、-1 C、1 D、55. 把一些笔记本分给几个学生,如果每人分3本,那么余8本,如果每人分5本,则最后一个人有分到本子但分到的本数不足3本,则共有学生( )人.A、4 B、5 C、6 D、5或66. 下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.②如果∠1和∠2是对顶角,那么∠1=∠2.③三角形的一个外角大于任何一个内角. ④如果 ,那么 .
A、1个 B、2个 C、3个 D、4个7. 若关于x的不等式组 无解,则a的取值范围为( )A、a<4 B、a≥4 C、a≤4 D、a>48. 如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )A、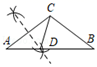 B、
B、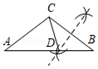 C、
C、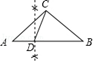 D、
D、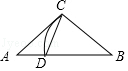 9. 如图,长方形ABCD中,点E是边CD的中点,将△ADE沿AE折叠得到△AFE,且点F在长方形ABCD内.将AF延长交边BC于点G.若BG=3CG,则 =( )
9. 如图,长方形ABCD中,点E是边CD的中点,将△ADE沿AE折叠得到△AFE,且点F在长方形ABCD内.将AF延长交边BC于点G.若BG=3CG,则 =( ) A、 B、1 C、 D、10. 如图所示,长方形ABCD中,AB=4,BC= ,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( )
A、 B、1 C、 D、10. 如图所示,长方形ABCD中,AB=4,BC= ,点E是折线ADC上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,使△PCB为等腰三角形的点E的位置共有( ) A、4个 B、5个 C、6个 D、不能确定
A、4个 B、5个 C、6个 D、不能确定二、填空填(本大题有6小题,每小题4分,共24分)
-
11. 若B地在A地的南偏东50°方向5 km处,则A地在B地的方向处.12. 已知正比例函数y=-2x,则当x=-1时,y= .13. 若x=2是关于x的不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是 .14. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y 轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为 .
 15. 如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 .
15. 如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第100个图形中等边三角形的个数是 . 16. 如图,在五边形 ABCDE 中, AB = AE = ,∠CAD = 45°,∠E=∠EAB =∠B =90°,点A到直线CD 的距离为
16. 如图,在五边形 ABCDE 中, AB = AE = ,∠CAD = 45°,∠E=∠EAB =∠B =90°,点A到直线CD 的距离为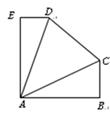
三、解答题(本大题有7小题,共66分)
-
17. 解不等式(组).(1)、 + ≥1(2)、18. 如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,请写出AB与DE之间的关系并证明你的结论.
 19. 已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.
19. 已知:△ABC与△A'B'C在平面直角坐标系中的位置如图. (1)、分别写出B、B'的坐标:B;B′;(2)、若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为;(3)、求△ABC的面积.20. 已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标.(1)、点P的横坐标比纵坐标大1;(2)、点P在过点A(3,-2),且与x轴平行的直线上;(3)、点P到y轴的距离是到x轴距离的2倍.21. 某校八年级举行英语词王争霸赛,购买A,B两种笔记本作为奖品.这两种笔记本的单价分别是12元和8元,根据比赛设奖情况需购买这两种笔记本共30本,并且所购买的A 种笔记本的数量多于B种笔记本数量,但又不多于B种笔记本数量的2倍,如果设他 们买A种笔记本n本,买这两种笔记本共花费w元.(1)、请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;(2)、若总共花费了320元,则A、B两种笔记本各买了几本?22. 已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.
(1)、分别写出B、B'的坐标:B;B′;(2)、若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为;(3)、求△ABC的面积.20. 已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标.(1)、点P的横坐标比纵坐标大1;(2)、点P在过点A(3,-2),且与x轴平行的直线上;(3)、点P到y轴的距离是到x轴距离的2倍.21. 某校八年级举行英语词王争霸赛,购买A,B两种笔记本作为奖品.这两种笔记本的单价分别是12元和8元,根据比赛设奖情况需购买这两种笔记本共30本,并且所购买的A 种笔记本的数量多于B种笔记本数量,但又不多于B种笔记本数量的2倍,如果设他 们买A种笔记本n本,买这两种笔记本共花费w元.(1)、请写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;(2)、若总共花费了320元,则A、B两种笔记本各买了几本?22. 已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.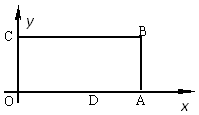 (1)、当t=5时, OP长为;(2)、当点P在BC边上时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;(3)、P在运动过程中,一定有△ODP是等腰三角形,求出P点坐标。23. 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)、当t=5时, OP长为;(2)、当点P在BC边上时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;(3)、P在运动过程中,一定有△ODP是等腰三角形,求出P点坐标。23. 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC. (1)、求证:BE=CF;(2)、在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.
(1)、求证:BE=CF;(2)、在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.