浙江省杭州市萧山区萧山区城区片六校2019-2020学年七年级上学期数学12月月考试卷

试卷更新日期：2019-12-31 类型：月考试卷

进入出卷网下载

一、单选题

1. 在 $0.01 ， \sqrt{15} ， - 5 ， - \frac{1}{5}$ 这四个数中,无理数的是（）

A、 $0.01$ B、 $\sqrt{15}$ C、 $- 5$ D、 $- \frac{1}{5}$

查看试题解析
2. 如果单项式 $2 x^{3} y^{4}$ 与 $- 2 x^{a} y^{2 b}$ 是同类项,那么 $a 、 b$ 的值分别是（）

A、3，2 B、2，2 C、3，4 D、2，4

查看试题解析
3. 下列计算正确的是（）

A、2﹣（﹣1）³＝2﹣1＝1 B、74﹣4÷70＝70÷70＝1 C、 $6 \div (\frac{1}{3} - \frac{1}{2}) = 6 \times 3 - 6 \times 2 = 6$ D、2³﹣3²＝8﹣9＝﹣1

查看试题解析
4. 把1.5952精确到十分位的近似数是（）

A、1.5 B、1.59 C、1.60 D、1.6

查看试题解析
5. 下列变形正确的是（）

A、由ac=bc，得a=b B、由 $\frac{a}{5} = \frac{b}{5} - 1$ ，得a=b﹣1 C、由2a﹣3=a，得a=3 D、由2a﹣1=3a+1，得a=2

查看试题解析
6. 下列计算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $3 a^{2} b - 3 b a^{2} = 0$ C、 $3 x^{2} + 2 x^{3} = 5 x^{5}$ D、 $3 y^{2} - 2 y^{2} = 1$

查看试题解析
7. 通过估算，估计 $\sqrt{73}$ 的大小应在（）

A、7～8之间 B、8.0～8.5之间 C、8.5～9.0之间 D、9～10之间

查看试题解析
8. 一项工程，甲独做需10天完成，乙单独做需15天完成，两人合作4天后，剩下的部分由乙独做全部完成，设乙独做x天，由题意得方程（）

A、 $\frac{4}{10}$ + $\frac{x - 4}{15}$ =1 B、 $\frac{4}{10}$ + $\frac{x + 4}{15}$ =1 C、 $\frac{x + 4}{10}$ + $\frac{4}{15}$ =1 D、 $\frac{x + 4}{10}$ + $\frac{x}{15}$ =1

查看试题解析
9. 对于有理数 $a 、 b ，$ 如果 $a b < 0 ， a + b < 0 ，$ 则下列各式成立的是（）

A、 $a < 0 ， b < 0$ B、 $a > 0 ， b < 0 且 | b | < a$ C、 $a < 0 ， b > 0 且 | a | < b$ D、 $a > 0 ， b < 0 且 | b | > a$

查看试题解析
10. 有两桶水，甲桶装有 $a$ 升水，乙桶中的水比甲桶中的水多3升.现将甲桶中倒一半到乙桶中，然后再将此时乙桶中总水量的 $\frac{1}{3}$ 倒给甲桶，假定桶足够大，水不会溢岀.我们将上述两个步骤称为一次操作，进行重复操作，则（）

A、每操作一次，甲桶中的水量都会减小，最后甲桶中的水会全部倒入乙桶 B、每操作一次，甲桶中的水量都会减小，但永远倒不完 C、每操作一次，甲桶中的水量都会增加，反复操作，最后甲桶中的水会比乙桶多 D、每操作一次，甲桶中的水量都会增加，但永远比乙桶中的水量要少

查看试题解析

二、填空题

11. “x的 $\frac{1}{3}$ 与y的差”用代数式可以表示为 .

查看试题解析
12. 若x是64的平方根，则 $\sqrt[3]{x}$ ＝ .

查看试题解析
13. 有理数a、b、c在数轴上的位置如图，则 $| a + c | + | c - b | - | a + b | =$ .

查看试题解析
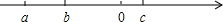14. 某公司有甲、乙两类经营收入，其中去年乙类收入为 $a$ 万元，去年甲类收入是乙类收入的2倍，预计今年甲类年收入减少9%，乙类收入将增加19%.今年该公司的年总收入比去年增加万元（用字母 $a$ 来表示）.

查看试题解析
15. 已知关于x的方程（m+2）x^|m+4|+x+18＝0是一元一次方程，m=.

查看试题解析
16. 从大拇指开始，按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指……的顺序，依次数整数1、2、3、4、5，6、7、…，当数到4019时对应的手指为；当第n次数到无名指时，数到的数是（用含n的代数式表示）.

查看试题解析

三、解答题

17. 字母a，b，c，d所表示的数如下表：

字母	a	b	c	d
字母表示的数	$\frac{9}{25}$ 的平方根	$\sqrt{7}$ 的相反数	$- （ \frac{4}{3} ）^{2} + 1 - （ - \frac{1}{3} ）^{3}$	单项式 $\frac{2 x^{2} y}{5}$ 的系数

(1)、直接写出上表中各字母所表示的数

(2)、计算（1）中最大数与最小数的差。

查看试题解析

18. 解下列方程:

(1)、 $3 - (4 x - 3) = 7$

(2)、 $\frac{x}{5} - \frac{3 - 2 x}{2} = x$

查看试题解析
19.

(1)、已知a＝﹣2，b＝﹣1，求（6a²+4ab）﹣2（3a²+ab﹣ $\frac{1}{2}$ b²）的值；

(2)、已知x²﹣xy＝﹣3，2xy﹣y²＝﹣8，求2x²+6xy﹣4y²的值.

查看试题解析
20. 先阅读下列解题过程，然后解答问题⑴、⑵，解方程： $| 3 x | = 1$ 。
解：①当3x≥0时，原方程可化为一元一次方程3x=1，它的解是 $x = \frac{1}{3}$ ；

②当3x≤0时，原方程可化为一元一次方程-3x=1，它的解是 $x = - \frac{1}{3}$ 。

(1)、请你根据以上理解，解方程： $2 | x - 3 | + 5 = 13$ ；

(2)、探究：当b为何值时，方程 $| x - 2 | = b + 1$ ，①无解；②只有一个解；③有两个解。

查看试题解析
21. 已知 ${(a + 3)}^{2} + \sqrt{b - 2} + | c + a | = 0$

(1)、分别写出a，b，c表示的数，并计算（a+b）+（b+c）+（c+a）的值；

(2)、设a，b，c在数轴上对应的点分别是点A，点B，点 C.若点M是线段AB上的一点，比较 $\frac{M A + M B}{5}$ 与MC的大小，说明理由.

查看试题解析
22. 某工厂加工齿轮，已知每1块金属原料可以加工成3个A齿轮或4个B齿轮（说明：每块金属原料无法同时既加工A齿轮又加B齿轮），已知1个A齿轮和2个B齿轮组成一个零件，为了加工更多的零件，要求A、B齿轮恰好配套.请列方程解决下列问题：

(1)、现有25块相同的金属原料，问最多能加工多少个这样的零件？

(2)、若把36块相同的金属原料全部加工完，问加工的A、B齿轮恰好配套吗？说明理由

(3)、若把n块相同的金属原料全部加工完，为了使这样加工出来的A、B齿轮恰好配套，请求出n所满足的条件.

查看试题解析
23. 如图，已知数轴上点A表示的数为﹣3，B是数轴上位于点A右侧一点，且AB＝12.动点P从点A出发，以每秒2个单位长度的速度沿数轴向点B方向匀速运动，设运动时间为t秒.

(1)、数轴上点B表示的数为；点P表示的数为（用含t的代数式表示）.

(2)、动点Q从点B出发，以每秒1个单位长度的速度沿数轴向点A方向匀速运动；点P、点Q同时出发，当点P与点Q重合后，点P马上改变方向，与点Q继续向点A方向匀速运动（点P、点Q在运动过程中，速度始终保持不变）；当点P返回到达A点时，P、Q停止运动.设运动时间为t秒.
①当点P返回到达A点时，求t的值，并求出此时点Q表示的数.
②当点P是线段AQ的三等分点时，求t的值.

查看试题解析