江苏省无锡市宜兴市宜城环科园联盟2020届九年级上学期数学12月月考试卷
试卷更新日期:2019-12-31 类型:月考试卷
一、单选题
-
1. 下列方程为一元二次方程的是 ( )A、x-2=0 B、x2-2x-3 C、xy+1=0 D、x2-4x-1=02. ⊙O的半径为R,圆心到点A的距离为d,且R、d是方程x2-6x+9=0的两根,则点A与⊙O的位置关系是 ( )A、点A在⊙O内 B、点A在⊙O上 C、点A在⊙O外 D、点A不在⊙O上3. 已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )A、20πcm2 B、20cm2 C、40πcm2 D、40cm24. 为了让宜兴市的山更绿、水更清,2016年市委、市政府提出了确保到2018年实现全市绿化覆盖率达到43%的目标,已知2016年绿化覆盖率为40 %,设从2016年起绿化覆盖率的年平均增长率为 ,则可列方程 ( )A、 % B、 C、 D、 %5. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( )
 A、
A、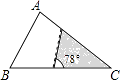 B、
B、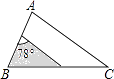 C、
C、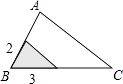 D、
D、 6. 关于 的方程 有实数根,则 满足( )A、 B、 且 C、 且 D、7. 如图, 且 则 =( )
6. 关于 的方程 有实数根,则 满足( )A、 B、 且 C、 且 D、7. 如图, 且 则 =( )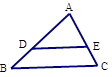 A、2︰ 1 B、1︰3 C、1︰8 D、1︰98. 在平面直角坐标系 中,直线经过点A(-3,0),点B(0, ),点P的坐标为(1,0),与 轴相切于点O,若将⊙P沿 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )A、1个 B、2个 C、3个 D、4个
A、2︰ 1 B、1︰3 C、1︰8 D、1︰98. 在平面直角坐标系 中,直线经过点A(-3,0),点B(0, ),点P的坐标为(1,0),与 轴相切于点O,若将⊙P沿 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 若 = ,则 = .10. 设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+mn+n2= .11. 将长为8cm的铁丝首尾相接围成半径为2cm的扇形,则S扇形=cm2.12. 已知线段AB=10,点C是线段AB上的黄金分割点(AC<BC),则AC长是(精确到0.01).13. 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=53o , 则∠BAC的度数等于.
 14. 在一张比例尺为1:50000的地图上,如果一块多边形地的周长是320cm,那么这块地的实际周长是km.15. 某同学掷出的铅球在平地上砸出一个直径约为10cm,深约为2cm的小坑,则该铅球的直径约为.16. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4 ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为.
14. 在一张比例尺为1:50000的地图上,如果一块多边形地的周长是320cm,那么这块地的实际周长是km.15. 某同学掷出的铅球在平地上砸出一个直径约为10cm,深约为2cm的小坑,则该铅球的直径约为.16. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4 ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为.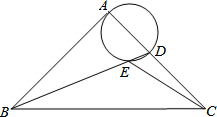
三、解答题
-
17. 解一元二次方程:(1)、(x+1)2-144=0(2)、x2-4x-32=0(3)、x(x﹣5)=2(x﹣5)(4)、18. △ABC在平面直角坐标系中的位置如图所示:
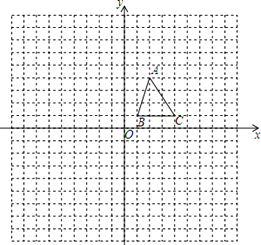 (1)、①画出△ABC关于x轴对称的△A1B1C1;
(1)、①画出△ABC关于x轴对称的△A1B1C1;②以原点O为位似中心,在y轴左侧将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请画出△A2B2C2;
(2)、设P(x,y)为△ABC内任意一点,△A2B2C2内的点P′是点P经过上述两次变换后的对应点,请直接写出P′的坐标.19. 如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O, (1)、求证:△EBC是等腰三角形;(2)、已知:AB=7,BC=5,求 的值.20. 已知: ABCD的两边AB,AD的长是关于x的方程 的两个实数根.(1)、当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)、若AB的长为2,那么 ABCD的周长是多少?21. 如图:△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)、求证:△EBC是等腰三角形;(2)、已知:AB=7,BC=5,求 的值.20. 已知: ABCD的两边AB,AD的长是关于x的方程 的两个实数根.(1)、当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)、若AB的长为2,那么 ABCD的周长是多少?21. 如图:△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.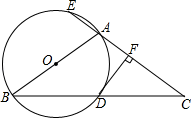 (1)、试说明DF是⊙O的切线;(2)、若AC=3AE,求DF:CF.22. 某商店经销甲、乙两种商品. 现有如下信息:
(1)、试说明DF是⊙O的切线;(2)、若AC=3AE,求DF:CF.22. 某商店经销甲、乙两种商品. 现有如下信息:
请根据以上信息,解答下列问题:
(1)、甲、乙两种商品的零售单价分别为元和元.(直接写出答案)(2)、该商店平均每天卖出甲商品500件和乙商品1200件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.为了使每天获取更大的利润,商店决定把甲种商品的零售单价下降x(x>0)元.在不考虑其他因素的条件下,当x定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?23. 如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF. (1)、当∠BAC=30º时,求△ABC的面积;(2)、当DE=8时,求线段EF的长;(3)、在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.
(1)、当∠BAC=30º时,求△ABC的面积;(2)、当DE=8时,求线段EF的长;(3)、在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.