湖北省孝感市孝南区十校联谊2019-2020学年八年级上学期数学12月月考试卷

试卷更新日期：2019-12-31 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图案是我国几家银行的标志，其中是轴对称图形的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 下列运算结果为 $a^{6}$ 的是 $($ $)$

A、 $a^{2} + a^{3}$ B、 $a^{2} \cdot a^{3}$ C、 ${(- a^{2})}^{3}$ D、 $a^{8} \div a^{2}$

查看试题解析
3. 一个多边形的每一个内角都等于150°，那么这个多边形的边数是（）

A、15 B、14 C、12 D、10

查看试题解析
4. 现有2cm，4 cm，5 cm，8 cm长的四根木棒，任选三根组成一个三角形，那么可以组成三角形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，给出下列四组条件：
①AB=DE，BC=EF，AC=DF；
②AB=DE，∠B=∠E．BC=EF；
③∠B=∠E，BC=EF，∠C=∠F；
④AB=DE，AC=DF，∠B=∠E．
其中，能使△ABC≌△DEF的条件共有（）

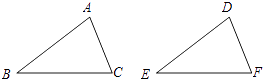A、1组 B、2组 C、3组 D、4组

查看试题解析
6. 下列计算正确的是（）

A、 $- 3 x^{2} y \cdot 5 x^{2} y = 2 x^{2} y$ B、 $35 x^{3} y^{2} \div 5 x^{2} y = 7 x y$ C、 $- 2 x^{2} y^{3} \cdot 2 x^{3} y = - 2 x^{5} y^{4}$ D、 $(- 2 x - y) (2 x + y) = 4 x^{2} - y^{2}$

查看试题解析
7. 下列计算正确的是（）

A、(x＋y)²＝x²＋y² B、(x－y)²＝x²－2xy－y² C、(－x＋1)(－x－1)＝x²－1 D、(x－1)²＝x²－1

查看试题解析
8. 如图，正方形 $A B C D$ 的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角板的两条直角边与 $C D$ 交于点F，与 $C B$ 延长线交于点E.四边形 $A E C F$ 的面积是（）.

A、16 B、12 C、8 D、4

查看试题解析
9. 小思同学用如图所示的A，B，C三类卡片若干张，拼出了一个长为2a＋b、宽为a＋b的长方形图形.请你通过计算求出小思同学拼这个长方形所用A，B，C三类卡片各（）张.

A、2张，1张，2张 B、3张，2张，1张 C、2张，1张，1张 D、3张，1张，2张

查看试题解析
10. 如图，△ABC是等边三角形，AQ＝PQ，PR⊥AB于点R，PS⊥AC于点S，PR＝PS，则下列结论：①AP⊥BC；②AS＝AR；③QP∥AR；④△BRP≌△QSP.正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若代数式2a²+3a+1的值是6，则代数式5－6a²－9a的值为；

查看试题解析
12. 若x²－kxy＋9y²是一个完全平方式，则k的值为.

查看试题解析
13. 一个等腰三角形的一个角为50°，则它的顶角的度数是．

查看试题解析
14. 一个正方形和两个等边三角形的位置如图所示，∠3=50°，则∠1+∠2=。

查看试题解析
15. 如图，在△ABC中，分别以点A和点B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB＝7，则△ABC的周长为．

查看试题解析
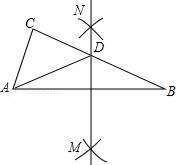16. 如图，在Rt△ABC中，∠C=90°，AC=10，BC=5，PQ=AB，点P和点Q分别在AC和AC的垂线AD上移动，则当AP=时，才能使△ABC和△APQ全等.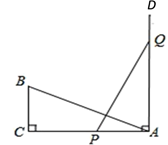

查看试题解析

三、解答题

17. 计算：

(1)、2019²－2018×2020；

(2)、0.125²⁰¹⁹×（－8²⁰²⁰）.

查看试题解析
18. 先化简，再求值

(1)、（a²b﹣2ab²﹣b³）÷b﹣（a+b）（a﹣b），其中a= $\frac{1}{2}$ ，b=﹣1.

(2)、6x²﹣（2x﹣1）（3x﹣2）+（x+2）（x﹣2），其中x=3.

查看试题解析
19. 如图，在ΔABC中，∠C=∠ABC=2∠A， BD是边AC上的高，求∠DBC的度数。

查看试题解析
20. 如图1，从边长为a的正方形纸片中剪去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸片拼成如图2的等腰梯形．

(1)、设图1中阴影部分面积为S₁ ，图2中阴影部分面积为S₂ ，请直接用含a，b的代数式表示S₁和S₂；

(2)、请写出上述过程所揭示的乘法公式．

查看试题解析
21. 已知a－b＝7，ab＝－10.求：

(1)、a²＋b²的值；

(2)、(a＋b)²＋2(a－b)²的值.

查看试题解析
22. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）.

①在如图所示的网格平面内作出平面直角坐标系；

②作出△ABC关于y轴对称的△A′B′C′，并写出点B′的坐标；

③P是x轴上的动点，在图中找出使△A′BP周长最短时的点P，直接写出点P的坐标.

查看试题解析
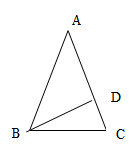
23. 如图，△ABC为等边三角形，D、E分别是边AC、BC上的点，且AD＝CE，AE与BD相交于点P.

(1)、求∠BPE的度数；

(2)、若BF⊥AE于点F，试判断BP与PF的数量关系并说明理由.

查看试题解析
24. 如图，等腰Rt△ABC中，∠ABC＝90°，AB＝BC，点A，B分别在坐标轴上.

(1)、如图1，若点C的横坐标为5，直接写出点B的坐标；

(2)、如图2，若点A的坐标为(－6，0)，点B在y轴的正半轴上运动时，分别以OB，AB为边在第一、第二象限作等腰Rt△OBF，等腰Rt△ABE，连接EF交y轴于点P，当点B在y轴的正半轴上移动时，PB的长度是否发生改变？若不变，求出PB的值；若变化，求PB的取值范围.

查看试题解析