重庆市大渡口区2019届数学中考二模试卷
试卷更新日期:2019-12-30 类型:中考模拟
一、单选题
-
1. 下列实数是负数的是( )A、0.1 B、-1 C、1 D、02. 下列图形,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列图形是用长度相等的火柴棒按一定规律排列的图形,第(1)个图形中有8根火柴棒,第(2)个图形中有14根火柴棒,第(3)个图形中有20根火柴棒,…,按此规律排列下去,第(6)个图形中,火柴棒的根数是( )
3. 下列图形是用长度相等的火柴棒按一定规律排列的图形,第(1)个图形中有8根火柴棒,第(2)个图形中有14根火柴棒,第(3)个图形中有20根火柴棒,…,按此规律排列下去,第(6)个图形中,火柴棒的根数是( ) A、34 B、36 C、38 D、484. 下列事件为不可能事件的是( )A、掷一枚质地均匀的正方体骰子,掷得的点数不是奇数就是偶数 B、从一副扑克牌中任意抽出一张,花色是黑桃 C、抛一枚普通的硬币,正面朝上 D、从装满红球的袋子中摸出一个白球5. 沿一张矩形纸较长两边中点将纸一分为二,所得两张矩形纸与原来的矩形纸相似,那么原来那张纸的长和宽的比是( )A、 B、 C、2:1 D、3:16. 下列命题是假命题的是( )A、三角形的三条高交于一点 B、直角三角形有三条高 C、三角形的一条中线把三角形的面积分成相等的两部分 D、三角形的三条中线交于一点7. 估计 的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 如图所示的运算程序中,若开始输入的x值为18,我们发现第一次输出的结果为9,第二次输出的结果为12,……,则第10次输出的结果为( )
A、34 B、36 C、38 D、484. 下列事件为不可能事件的是( )A、掷一枚质地均匀的正方体骰子,掷得的点数不是奇数就是偶数 B、从一副扑克牌中任意抽出一张,花色是黑桃 C、抛一枚普通的硬币,正面朝上 D、从装满红球的袋子中摸出一个白球5. 沿一张矩形纸较长两边中点将纸一分为二,所得两张矩形纸与原来的矩形纸相似,那么原来那张纸的长和宽的比是( )A、 B、 C、2:1 D、3:16. 下列命题是假命题的是( )A、三角形的三条高交于一点 B、直角三角形有三条高 C、三角形的一条中线把三角形的面积分成相等的两部分 D、三角形的三条中线交于一点7. 估计 的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间8. 如图所示的运算程序中,若开始输入的x值为18,我们发现第一次输出的结果为9,第二次输出的结果为12,……,则第10次输出的结果为( ) A、0 B、3 C、5 D、69. 如图, 是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆 的顶端 处有一探射灯,射出的边缘光线 和 与水平路面 所成的夹角 和 分别是37°和60°(图中的点 均在同一平面内, ).则 的长度约为( )(结果精确到0.1米,)参考数据:( =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A、0 B、3 C、5 D、69. 如图, 是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆 的顶端 处有一探射灯,射出的边缘光线 和 与水平路面 所成的夹角 和 分别是37°和60°(图中的点 均在同一平面内, ).则 的长度约为( )(结果精确到0.1米,)参考数据:( =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)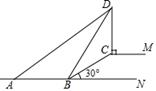 A、9.4米 B、10.6米 C、11.4米 D、12.6米10. 如图,已知等腰 ,以 为直径的圆交 于点 ,过点 的⊙ 的切线交 于点 ,若 ,则⊙ 的半径是( )
A、9.4米 B、10.6米 C、11.4米 D、12.6米10. 如图,已知等腰 ,以 为直径的圆交 于点 ,过点 的⊙ 的切线交 于点 ,若 ,则⊙ 的半径是( )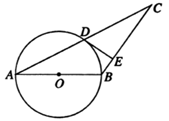 A、 B、5 C、6 D、11. 如图,已知四边形 的边 在 轴上, ,过点 的双曲线 交 于 ,且 ,若 的面积等于3,则 的值等于( )
A、 B、5 C、6 D、11. 如图,已知四边形 的边 在 轴上, ,过点 的双曲线 交 于 ,且 ,若 的面积等于3,则 的值等于( )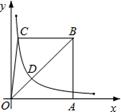 A、2 B、 C、 D、12. 如果关于 的不等式组 的解集为 ,且关于 的分式方程 有非负数解,则所有符合条件的整数 的值之和是( )A、-2 B、-1 C、0 D、2
A、2 B、 C、 D、12. 如果关于 的不等式组 的解集为 ,且关于 的分式方程 有非负数解,则所有符合条件的整数 的值之和是( )A、-2 B、-1 C、0 D、2二、填空题
-
13. 计算: .14. 如图,在半径为2 的 中,点 、点 是弧 的三等分点,点 是直径 的延长线上一点, ,则图中阴影部分的面积是(结果保留 ).
 15. 十八世纪法国有名的数学家达兰倍尔犯了这样一个错误:拿两枚硬币随意抛掷,会出现三种情况,要么两枚都是正面向上,要么一枚正面向上,一枚背面向上,要么两枚都是背面向上,因此,两枚都是正面向上的概率是 .事实上,两枚硬币都是正面向上的概率应该是.16. 如图,矩形 中, ,点 为 上一点,将 沿 折叠得到 ,点 为 上一点,将 沿 折叠得到 ,且 落在线段 上,当 时,则 的长为.
15. 十八世纪法国有名的数学家达兰倍尔犯了这样一个错误:拿两枚硬币随意抛掷,会出现三种情况,要么两枚都是正面向上,要么一枚正面向上,一枚背面向上,要么两枚都是背面向上,因此,两枚都是正面向上的概率是 .事实上,两枚硬币都是正面向上的概率应该是.16. 如图,矩形 中, ,点 为 上一点,将 沿 折叠得到 ,点 为 上一点,将 沿 折叠得到 ,且 落在线段 上,当 时,则 的长为.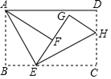 17. 松松和东东骑自行车分别从迎宾大道上相距9500米的A、B两地同时出发,相向而行,行驶一段时间后松松的自行车坏了,立刻停车并马上打电话通知东东,东东接到电话后立刻提速至原来的 倍,碰到松松后用了5分钟修好了松松的自行车,修好车后东东立刻骑车以提速后的速度继续向终点A地前行,松松则留在原地整理工具,2分钟以后松松以原速向B走了3分钟后,发现东东的包在自己身上,马上掉头以原速的 倍的速度回A地;在整个行驶过程中,松松和东东均保持匀速行驶(东东停车和打电话的时间忽略不计),两人相距的路程S(米)与松松出发的时间t(分钟)之间的关系如图所示,则东东到达A地时,松松与A地的距离为米.
17. 松松和东东骑自行车分别从迎宾大道上相距9500米的A、B两地同时出发,相向而行,行驶一段时间后松松的自行车坏了,立刻停车并马上打电话通知东东,东东接到电话后立刻提速至原来的 倍,碰到松松后用了5分钟修好了松松的自行车,修好车后东东立刻骑车以提速后的速度继续向终点A地前行,松松则留在原地整理工具,2分钟以后松松以原速向B走了3分钟后,发现东东的包在自己身上,马上掉头以原速的 倍的速度回A地;在整个行驶过程中,松松和东东均保持匀速行驶(东东停车和打电话的时间忽略不计),两人相距的路程S(米)与松松出发的时间t(分钟)之间的关系如图所示,则东东到达A地时,松松与A地的距离为米. 18. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇0.5小时后,第二列快车与慢车相遇.则第二列快车比第一列快车晚出发小时.
18. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇0.5小时后,第二列快车与慢车相遇.则第二列快车比第一列快车晚出发小时.
三、解答题
-
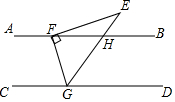
19.(1)、(2)、化简:20. 如图,AB∥CD,△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
 21. 某地区九年级学生参加学业水平质量监测。随机抽取其中25名学生的成绩(满分为100分),统计如下:
21. 某地区九年级学生参加学业水平质量监测。随机抽取其中25名学生的成绩(满分为100分),统计如下:90,74,88,65,98,75,81,42,85,70,55,80,95,88,72,88,60,56,76,66,78,72,82,63,100.
(1)、90分及以上为 级,75—89分为 级,60—74分为 级,60分以下为 级。请把下面表格补充完整:等级
人数
8
(2)、根据(1)中完成的表格,可知这组数据的极差是 , 中位数是 , 众数是.(3)、该地区某学校九年级共有1000名学生,如果60分及以上为及格,请估计该校九年级参加此次学业水平质量监测有多少人及格?(4)、若要知道抽测中每一个等级的人数占总人数的百分比,应选择统计图.22. 如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),已知直线l:y= x﹣2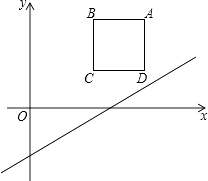 (1)、将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值(2)、在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.23. 某建材销售公司在2019年第一季度销售 两种品牌的建材共126件, 种品牌的建材售价为每件6000元, 种品牌的建材售价为每件9000元.(1)、若该销售公司在第一季度售完两种建材后总销售额不低于96.6万元,求至多销售 种品牌的建材多少件?(2)、该销售公司决定在2019年第二季度调整价格,将 种品牌的建材在上一个季度的基础上下调 , 种品牌的建材在上一个季度的基础上上涨 ;同时,与(1)问中最低销售额的销售量相比, 种品牌的建材的销售量增加了 , 种品牌的建材的销售量减少了 ,结果2019年第二季度的销售额比(1)问中最低销售额增加 ,求 的值.24. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)、将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值(2)、在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.23. 某建材销售公司在2019年第一季度销售 两种品牌的建材共126件, 种品牌的建材售价为每件6000元, 种品牌的建材售价为每件9000元.(1)、若该销售公司在第一季度售完两种建材后总销售额不低于96.6万元,求至多销售 种品牌的建材多少件?(2)、该销售公司决定在2019年第二季度调整价格,将 种品牌的建材在上一个季度的基础上下调 , 种品牌的建材在上一个季度的基础上上涨 ;同时,与(1)问中最低销售额的销售量相比, 种品牌的建材的销售量增加了 , 种品牌的建材的销售量减少了 ,结果2019年第二季度的销售额比(1)问中最低销售额增加 ,求 的值.24. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.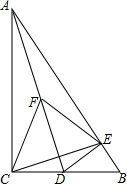 (1)、连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由(2)、若BD= CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.25. 数学综合实践课上,老师提出问题:如图,有一张长为4dm,宽为3dm的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究:
(1)、连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由(2)、若BD= CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.25. 数学综合实践课上,老师提出问题:如图,有一张长为4dm,宽为3dm的长方形纸板,在纸板四个角剪去四个相同的小正方形,然后把四边折起来(实线为剪裁线,虚线为折叠线),做成一个无盖的长方体盒子,问小正方形的边长为多少时,盒子的体积最大?为了解决这个问题,小明同学根据学习函数的经验,进行了如下的探究: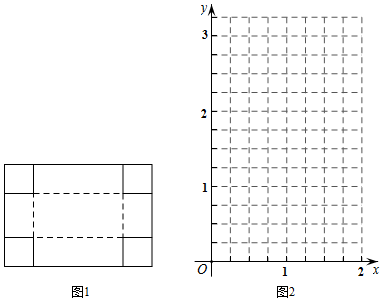 (1)、设小正方形的边长为xdm,长方体体积为ydm3 , 根据长方体的体积公式,可以得到y与x的函数关系式是,其中自变量x的取值范围是.(2)、列出y与x的几组对应值如下表:
(1)、设小正方形的边长为xdm,长方体体积为ydm3 , 根据长方体的体积公式,可以得到y与x的函数关系式是,其中自变量x的取值范围是.(2)、列出y与x的几组对应值如下表:x/dm
…
1
…
y/dm3
…
1.3
2.2
2.7
3.0
2.8
2.5
1.5
0.9
…
(注:补全表格,保留1位小数点)
(3)、如图,请在平面直角坐标系中描出以补全后表格中各对对应值为坐标的点,画出该函数图象;26. 如图,抛物线y=- [(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.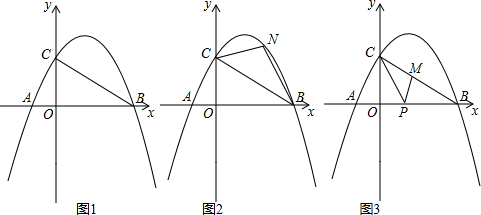 (1)、求m、n的值;(2)、如图,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;(3)、如图,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求m、n的值;(2)、如图,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;(3)、如图,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.